Skip over navigation
The dice has been rolled around without sliding, and it has printed the picture below. Your challenge is to find where the cube was placed to begin with and map out the route it has travelled. You may find it useful to print off a copy of the picture on this sheet.
There are two different ways of arranging the numbers on the faces of dice. If you look at the faces '1', '2' and '3' on a dice, you can see that they share a vertex. In a left-handed dice, the '1', '2' and '3' run clockwise, and in a right-handed dice they go anti-clockwise. See Right or Left? for more information about this. If you're using a dice for this activity, first work out which type of dice you have and then use the matching print below.
Right-handed dice print:
”‹
Left-handed dice print:
Rolling That Cube
Age 5 to 11
Challenge Level 
Rolling That Cube
We have a dice with raised spots, which have been pressed on an ink pad.
We start by printing one number.
Can you see how the numbers below have been printed by rolling the dice in the four different directions?
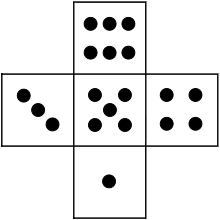
We start by printing one number.
Can you see how the numbers below have been printed by rolling the dice in the four different directions?
The dice has been rolled around without sliding, and it has printed the picture below. Your challenge is to find where the cube was placed to begin with and map out the route it has travelled. You may find it useful to print off a copy of the picture on this sheet.
There are two different ways of arranging the numbers on the faces of dice. If you look at the faces '1', '2' and '3' on a dice, you can see that they share a vertex. In a left-handed dice, the '1', '2' and '3' run clockwise, and in a right-handed dice they go anti-clockwise. See Right or Left? for more information about this. If you're using a dice for this activity, first work out which type of dice you have and then use the matching print below.
Right-handed dice print:
”‹ Why do this problem?
This activity is useful for developing good spatial awareness and offers opportunities for sharing different ways of approaching it.
Possible approach
Depending on the pupils' experiences, it may be appropriate to start with them all together with a practical example. Using a large dice, they could observe what happens as it rolls and try to predict what face will be at the bottom each time. Show children the picture of the prints which go in four different directions from the centre number, and encourage them to describe what has
happened. Can they roll the large dice to show how these prints have been made?
You could then present the challenge itself and give children time to work independently or in pairs. A copy of the route can be found on this sheet (word, pdf). Try not to direct the way they work as you may be suprised by the methods they choose.
The plenary can then focus on their different approaches. Allow time for all the different ways to be explained and then encourage pairs/small groups to discuss which method they might use if they were presented with a similar problem. Can they justify their choice?
You may be surprised by those learners who find this task challenging and need extra support and those who don't.
You may be surprised by those learners who find this task challenging and need extra support and those who don't.
Key questions
When working with the simple cube above:
What's happening here?
What can you tell me about the one at the bottom when I roll it this way?
When working on the actual challenge:
How are you working this out?
Is there more than one way of getting there?
Possible extension
When pupils have managed this activity in a confident way they may like to have a look at Inky Cube which is similar but much harder. You could also give the pupils opportunities to create their own cubes and set challenges for each other.
Possible support
Some pupils will need practice in carefully rolling the dice.
You may also like
Plants
Three children are going to buy some plants for their birthdays. They will plant them within circular paths. How could they do this?
Triangle Animals
How many different ways can you find to join three equilateral triangles together? Can you convince us that you have found them all?
Junior Frogs
Have a go at this well-known challenge. Can you swap the frogs and toads in as few slides and jumps as possible?