Rolling That Cube

This activity produced a few replies. Oliver from St. Anthony's sent in;

R R D L L D D R R U L

Tessa, Sally and Kensa from Sherwood State School in Australia sent in their solution like this;

$1, 4, 6, 2, 4, 5, 1, 2, 4, 5, 1, 4$
 

Hanako and Emilia at Vale Junior School, Guernsey sent in this word document;

First we decided to make a cube to physically test our theories and ideas.
We spotted that there were two impossible routes. These were: the $4$s down the middle and the $1, 4, 1$ combination going across.
These are impossible because you can't have two $4$s next to each other as there is only one four on the dice. The other is impossible as to get from $1$ to $4$, and then to $1$ again, you would have to double back on yourself.
Next, we had to think of a route that bypassed these two impossible combinations. We thought that we could start our route with the $4$ in the impossible $1, 4, 1$ combination so that we didn't have to complete the whole impossible combination.
 

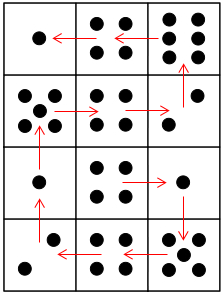
We checked that our theory was correct by rolling our cube along the grid. As we rolled it, we wrote the next number in the grid as a reflection on the next face of the cube. We tried starting at the top $1$ and the centre $4$ and we found that this route works both ways.
 

Thank you Hanaho and Emilia for explaining how you did it and what your thoughts were and well done all of you!