Skip over navigation
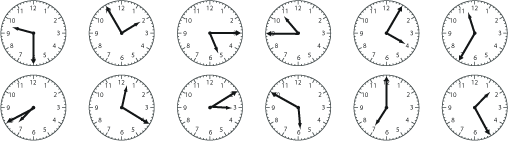
You can get a copy of these clock times which can be printed out and cut into separate cards.
The same times - in words - are on this sheet.
Printable NRICH Roadshow resource.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
What Is the Time?
Age 5 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
What Is the Time?
Can you put the times on these clocks in order?
You can get a copy of these clock times which can be printed out and cut into separate cards.
The same times - in words - are on this sheet.
Printable NRICH Roadshow resource.
Why do this problem?
This problem assesses and extends children's understanding of "telling the time", which is really reading the clock. Many children have difficulties with this, which is not surprising when you realise that analogue clocks are two dials superimposed on one another.
This problem only uses times which are exactly on the numbers relating to five minute intervals, and is best attempted once children are familiar with which hand is which, and what each one indicates.
Possible approach
The clock pictures can be downloaded here (word, pdf) and the time in words here (word, pdf). These can be printed (and possibly laminated), then cut into separate cards. You could provide a set of cards for each pair, or they could be enlarged and used by a group of up to four children. This sheet (word, pdf) of empty clock faces could be useful.
This task is probably best introduced with a minimum of teacher talk. Simply give each pair or group the cards and invite them to order the clock faces. The time in words can also be arranged to accompany the clock pictures. Give them plenty of time to tackle the challenge and try to step back. You may wish to stop them after some time to discuss what they have done so far
so that ideas are shared among the whole class.
In the plenary, encourage children to explain how they went about the task, rather than only focusing on their final answer. Listen out for children who realise that the hour hand is the hand to look at first. If there are disagreements about the order, invite pairs or groups to try and justify their thinking. None of the clocks or the written times mentions am/pm so
it will be interesting to see how the children cope with this and whether it comes up in their conversations.
Key questions
What does that hand tell you?
Which of these two clocks shows the earliest time? How do you know?
Possible extension
Learners could do the harder related problem The Time Is ... or make up their own problem cards using this sheet.Possible support
It may be helpful to have a demonstration clock or clocks with gears available.You may also like
Triangle Animals
How many different ways can you find to join three equilateral triangles together? Can you convince us that you have found them all?
Triple Cubes
This challenge involves eight three-cube models made from interlocking cubes. Investigate different ways of putting the models together then compare your constructions.
The Add and Take-away Path
Two children made up a game as they walked along the garden paths. Can you find out their scores? Can you find some paths of your own?

