Bent Out of Shape

• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science

When a molecule consists of one central atom with several others covalently bonded to it the electrons in these bonds repel each other. The result of this is that the bonded atoms will be oriented as far away from each other as possible, eg.
 
 
 
The angle formed between the two oxygen atoms (the "bond angle") is $180^\circ$ - given that the length of the bonds are fixed the oxygen atoms could not be further apart.
 

 
 Here, the central boron has three fluorine atoms bonded to it. The angle between any two fluorines is the same and it is $120^\circ$ . Again, the three F atoms could not have arranged themselves to be further apart.
 
This occurs because the bonds are formed of pairs of electrons, which carry a negative charge. If two bodies (in this case bonds) are negatively charged they will repel each other.
 
Draw diagrams to represent the structures of the following molecules. Can you work out what the bond angles are? (You don't need to know anything about the molecules!)
 
NH$_{4}^{+}$
CH$_{4}$
BeH$_{2}$
AlCl$_{3}$
PCl$_{5}$
SF$_{6}$
 
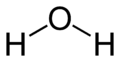
Water (H$_{2}$O) has a bond angle of $104.5^\circ$. What would you have expected the bond angle to be? Why do you think it might be different?


 
Similarly, NH$_{3}$ has a bond angle of $107.5^\circ$. As is the case for water, this is because the nitrogen atom has an unbonded pair of electrons in its outer shell - a lone pair. This acts much like a bond, repelling the electrons in the covalent bonds. Why do you think the bond angle is not the same as for NH$_{4}$? Draw the two molecules side by side. How does the orientation of the hydrogen atoms differ? How many covalent bonds is the lone pair here equivalent to in terms of repulsive effect? Is this the same as for the lone pairs in water? Does this surprise you?