Biology Measurement Challenge

• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

Consider these objects, images for which are given below:

1. Mitochondria
2. Arabis voch pollen
3. Ring stage of Plasmodium falciparum
4. Tuberculosis bacterium
5. Human red blood cell
6. Human nerve cell
7. The eye of a needle
8. Cat hair
9. Snowflake crystal

How many do you recognise? Can you put them in order of length? Cross-sectional area? Volume? Once in order, how many of the smaller objects would fit into the larger objects?
 
Discussion point: What measurement difficulties does this task raise?
 
 
You can see the images, some of which contain scale information, below

Mitochondria



Arabis voch pollen



Ring stage of Plasmodium falciparum



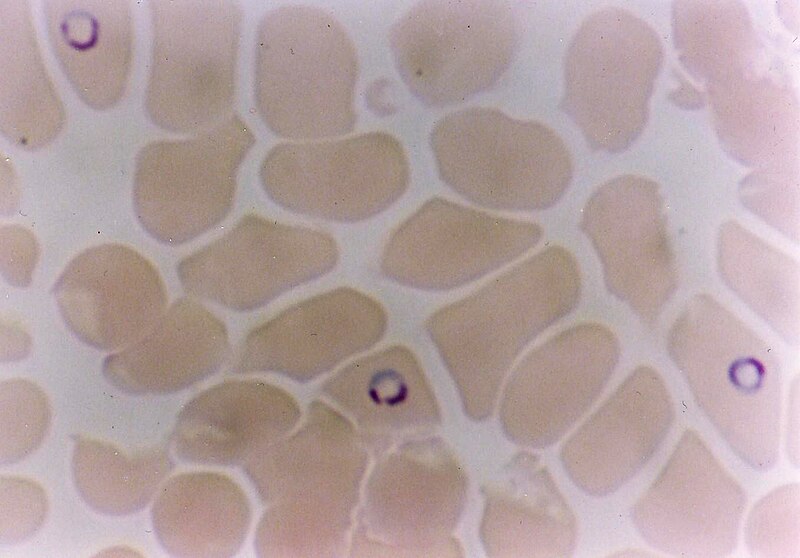
Tuberculosis bacterium



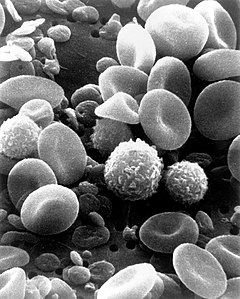
Human red blood cell



Human nerve cell

 

The eye of a needle

<missing image>

Cat hair



Snowflake Crystal



The URLS of these beautiful images are as follows:

 

• Mitochondria - https://commons.wikimedia.org/wiki/File:Mitochondria,_mammalian_lung_-_TEM_%282%29.jpg
• Arabis voch Pollen - https://commons.wikimedia.org/wiki/File:Arabis_voch1-1.jpg  
• Plasmodium falciparum - https://commons.wikimedia.org/wiki/File:Plasmodium_falciparum_in_Red_Blood_Cells.jpg
• Bacterium (tuberculosis) - https://commons.wikimedia.org/wiki/File:Mycobacterium_tuberculosis_8438_lores.jpg    
• Human red blood  - https://commons.wikimedia.org/wiki/File:SEM_blood_cells.jpg
• Nerve cell - https://commons.wikimedia.org/wiki/File:Myelinated_neuron.jpg
• Eye of a needle - https://commons.wikimedia.org/wiki/File:Eye_of_a_Needle.jpg
• Cat hair - https://commons.wikimedia.org/wiki/File:ESEM_BSE_cat_hair_No1194_10kV_1000x_680Pa.jpg
• Snow crystals - png: https://commons.wikimedia.org/wiki/File:Snow_crystals.png