Factor Track

Factor Track

Factor Track is not a race but a game of skill.
Below is a simple training version. The idea is to go round the track in as few turns as possible, keeping to the rules.
 

 

 
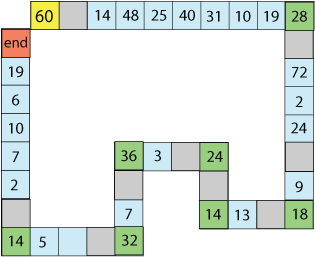
Rules:
You start on the (yellow) 60 and must make your way round to the (red) 'end' square.
You can move any factor of the number you are on, except 1.
You must land exactly on each green square, so you can't go round corners in one turn.
 
Have a go at moving round this 'training' track following the rules.  
Can you do it in fewer turns?

When you feel ready, try this more complicated track where there are possible short cuts. You will have to work out whether they are worthwhile.

 

 

 

 

 

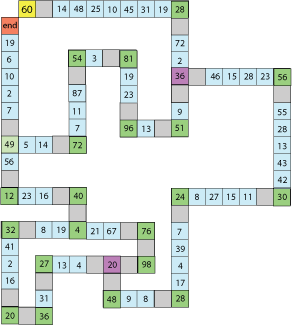
You might find it easier to print out this larger copy of the track which also has the rules on it.

You can do this on your own or with a friend. Who can get round in the least number of turns?

What is the best route to take to do it in the least number of turns?
Which squares do you need to land on?

Printable NRICH Roadshow resource.

 

Why do this problem?

This problem will help to improve learners' knowledge of factors, especially those in the usual multiplication tables, and encourages them to use trial and improvement.  The competitive element can bring out the best in some pupils.

Possible approach

You could start by showing the group the 'training track' given in the problem, working on this so that they are able to see the rules in action. This sheet has the 'training track' on, if you want it.  Once they have had a go, you could spend a short time discussing the reasons for their choices and ultimately the minimum number of turns that will take you round the track. 

Key questions
 

Possible extension

Learners could make their own 'factor track' for others to try.  Alternatively, the problem Factor-multiple Chains offers another interesting way to explore factors.

Possible support

You could suggest  that learners record all factors of the number in green squares so they are able to keep track of the ones they have tried more easily. The problem Jumping Squares has the same idea of getting round a track in as few turns as possible but focuses on counting, rather than factors.