Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Jumping Squares
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everyone who had a go at this.
Here are some of your solutions.
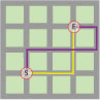
Kimberley managed to get round in 12 moves:
(All moves are forward) You start on 1\3 so if you move 1 that takes you to 4\1 (1 move). Then, move 4 places which takes you to 0\1 (2). After that, move 1 space to another 0\1 (3 moves). Then move the following numbers, 1 (4 moves), 3 (5 moves), 2 (6 moves), 2 (7 moves), 4 (8 moves), 4 (9 moves), 2 (10 moves), 1 (11 moves), then finally move the final 4 spaces (12 moves) and you come to the end.
Nicholas from Purleigh did the same route but made a mistake on his first go so he counted on before deciding which number to move to on his second go.
Jonah, Class 9a (Angmering), Erin (Wingate Primary) and Indi (Broomfields Junior School) all did it in 11 moves.
Here, Abby and Claire (Springfield Primary School) explain how they did it:
First we went forward 3 and that led us to a square that said 1/3. Then we went forward 3 again which took us to 1/0. So we went forward 1 and that led us to 4/3. Then we just went forward 3 not 4 which took us to 3/2. Then we went forward 2 which led us to 2/1. So then we went forward 2 so that we didnt land on 0/0. we ended up on 4/0. Now we go forward 4 that led us to 1/4. Then we went forward 4 which led us to2/2. So we went forward 1 which led us to to 4/1. Then we went forward 4 which led us to the end!!! So in the end we went round the track in 11 moves.
James, Emerald and Chris from Myland Primary School told us about their methods:
We tried only going forwards. These are some of the routes that get from the start to the end.
Start 3, 3, 1, 3, 2, 2, 4, 4, 2, 1, 4, end
Start 3, 3, 1, 3, 2, 2, 4, 4, 2, 1, 1, 3 end
Start 1, 4, 1, 1, 3, 2, 2, 4, 4, 2, 1, 4, end
Start 1, 4, 1, 1, 3, 2, 2, 4, 4, 2, 1, 1, 3 end
Start 1, 1, 2, 2, 1, 3, 2, 2, 4, 4, 2, 1, 4, end
Start 1, 1, 2, 2, 1, 3, 2, 2, 4, 4, 2, 1, 1, 3 end
We tried all the starting combinations with 1 and 3. We found that no matter what numbers you chose you always land on the square 4/3. Then if you choose 4 then you get stuck at 0/0, so you have to move 3 onto 3/2. If you choose 3 you land on 0/0, so you have to move 2. The middle part of the route is always the same 3, 2, 2, 4, 4, 2, 1. The quickest way to get to 4/3 is 3, 3, 1 or 3, 1, 3. The quickest way to end is to choose 4 on square 4/1 near the end. We had different strategies and tried out different ideas.
James: "With only forwards moves it is impossible to land on the squares 3/1, 2/1, 2/3, 2/4, 1/0, 3/3, 3/0, 0/1."
Chris: "I tried getting back to the start from the 2/4 square near the end. It wasn't possible, I always ended up on the 0/0s. 2/3, 2/2, 2/1 and 3/1 to the left of the end square were dead ends and there is no way of jumping over them."
Emerald: "I didn't like to land on a square with a zero, because then I didn't have a choice." "Going backwards you will always end up on 0/0, no matter which of the inside squares you start on."
Indigo class from Unicorn tried something a bit different:
Jo, Ollie, Rudi, Freya, Oliver and Joseph tackled the problem. They worked in pairs moving a counter around the board. To begin with they just said how many moves they could do it in but hadn't recorded it. They then came up with the method of moving the counter and recording the jumps on a piece of paper. The least number of jumps they all did it in was 11 with no jumps backwards.
+3 +3 +1 +3 +2 +2 +4 +4 +2 +1 +4 (everyone got this solution)
Joseph and Oliver investigated starting with +1 followed by +4 but this resulted in 12 jumps. The last 8 jumps are the same as the first sequence of jumps but they have 4 moves before this rather than 3.
+1 +4 +1 +1 +3 +2 +2 +4 +4 +2 +1 +4
Jo was quick to spot that you didn't want to land on the box with 2/0 in it in the bottom row as going forward 2 put you on a 0/0 box. Going back 2 put you on 2/4 box so you then had to go back 4 and so on therefore adding in lots of extra jumps!
They discussed the possibility of doing it in less than 11 moves but realised that in each case bar one they had moved the maximum number of spaces. They had to choose 3 moves instead of 4 moves at the bottom of the first column to avoid the situation described by Jo above.
Kimberley managed to get round in 12 moves:
(All moves are forward) You start on 1\3 so if you move 1 that takes you to 4\1 (1 move). Then, move 4 places which takes you to 0\1 (2). After that, move 1 space to another 0\1 (3 moves). Then move the following numbers, 1 (4 moves), 3 (5 moves), 2 (6 moves), 2 (7 moves), 4 (8 moves), 4 (9 moves), 2 (10 moves), 1 (11 moves), then finally move the final 4 spaces (12 moves) and you come to the end.
Nicholas from Purleigh did the same route but made a mistake on his first go so he counted on before deciding which number to move to on his second go.
Jonah, Class 9a (Angmering), Erin (Wingate Primary) and Indi (Broomfields Junior School) all did it in 11 moves.
Here, Abby and Claire (Springfield Primary School) explain how they did it:
First we went forward 3 and that led us to a square that said 1/3. Then we went forward 3 again which took us to 1/0. So we went forward 1 and that led us to 4/3. Then we just went forward 3 not 4 which took us to 3/2. Then we went forward 2 which led us to 2/1. So then we went forward 2 so that we didnt land on 0/0. we ended up on 4/0. Now we go forward 4 that led us to 1/4. Then we went forward 4 which led us to2/2. So we went forward 1 which led us to to 4/1. Then we went forward 4 which led us to the end!!! So in the end we went round the track in 11 moves.
James, Emerald and Chris from Myland Primary School told us about their methods:
We tried only going forwards. These are some of the routes that get from the start to the end.
Start 3, 3, 1, 3, 2, 2, 4, 4, 2, 1, 4, end
Start 3, 3, 1, 3, 2, 2, 4, 4, 2, 1, 1, 3 end
Start 1, 4, 1, 1, 3, 2, 2, 4, 4, 2, 1, 4, end
Start 1, 4, 1, 1, 3, 2, 2, 4, 4, 2, 1, 1, 3 end
Start 1, 1, 2, 2, 1, 3, 2, 2, 4, 4, 2, 1, 4, end
Start 1, 1, 2, 2, 1, 3, 2, 2, 4, 4, 2, 1, 1, 3 end
We tried all the starting combinations with 1 and 3. We found that no matter what numbers you chose you always land on the square 4/3. Then if you choose 4 then you get stuck at 0/0, so you have to move 3 onto 3/2. If you choose 3 you land on 0/0, so you have to move 2. The middle part of the route is always the same 3, 2, 2, 4, 4, 2, 1. The quickest way to get to 4/3 is 3, 3, 1 or 3, 1, 3. The quickest way to end is to choose 4 on square 4/1 near the end. We had different strategies and tried out different ideas.
James: "With only forwards moves it is impossible to land on the squares 3/1, 2/1, 2/3, 2/4, 1/0, 3/3, 3/0, 0/1."
Chris: "I tried getting back to the start from the 2/4 square near the end. It wasn't possible, I always ended up on the 0/0s. 2/3, 2/2, 2/1 and 3/1 to the left of the end square were dead ends and there is no way of jumping over them."
Emerald: "I didn't like to land on a square with a zero, because then I didn't have a choice." "Going backwards you will always end up on 0/0, no matter which of the inside squares you start on."
Indigo class from Unicorn tried something a bit different:
Jo, Ollie, Rudi, Freya, Oliver and Joseph tackled the problem. They worked in pairs moving a counter around the board. To begin with they just said how many moves they could do it in but hadn't recorded it. They then came up with the method of moving the counter and recording the jumps on a piece of paper. The least number of jumps they all did it in was 11 with no jumps backwards.
+3 +3 +1 +3 +2 +2 +4 +4 +2 +1 +4 (everyone got this solution)
Joseph and Oliver investigated starting with +1 followed by +4 but this resulted in 12 jumps. The last 8 jumps are the same as the first sequence of jumps but they have 4 moves before this rather than 3.
+1 +4 +1 +1 +3 +2 +2 +4 +4 +2 +1 +4
Jo was quick to spot that you didn't want to land on the box with 2/0 in it in the bottom row as going forward 2 put you on a 0/0 box. Going back 2 put you on 2/4 box so you then had to go back 4 and so on therefore adding in lots of extra jumps!
They discussed the possibility of doing it in less than 11 moves but realised that in each case bar one they had moved the maximum number of spaces. They had to choose 3 moves instead of 4 moves at the bottom of the first column to avoid the situation described by Jo above.
You may also like
Triangle Animals
How many different ways can you find to join three equilateral triangles together? Can you convince us that you have found them all?
Triple Cubes
This challenge involves eight three-cube models made from interlocking cubes. Investigate different ways of putting the models together then compare your constructions.
The Add and Take-away Path
Two children made up a game as they walked along the garden paths. Can you find out their scores? Can you find some paths of your own?

