Polygonals

Polygonal numbers are those that are arranged in shapes as they enlarge (starting with $1$). Here are examples of the $5$th polygonal numbers for the first $7$ shapes Triangle ($3$) through to Nonegon ($9$).

 

There is another group that are called "Centred Polygonals"  that look like these; 

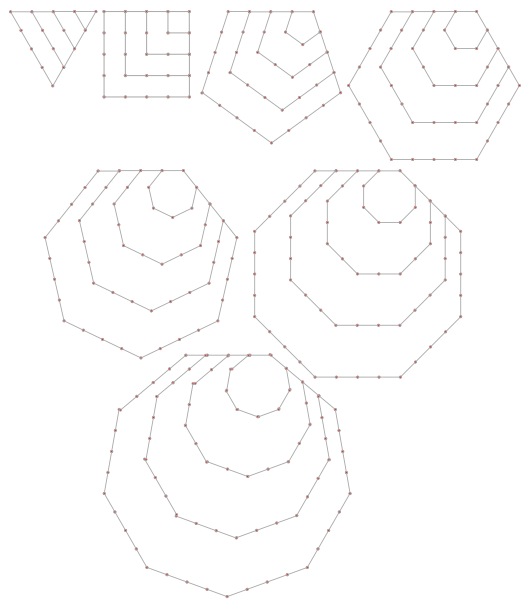
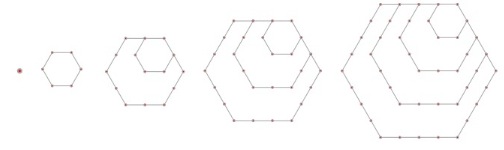
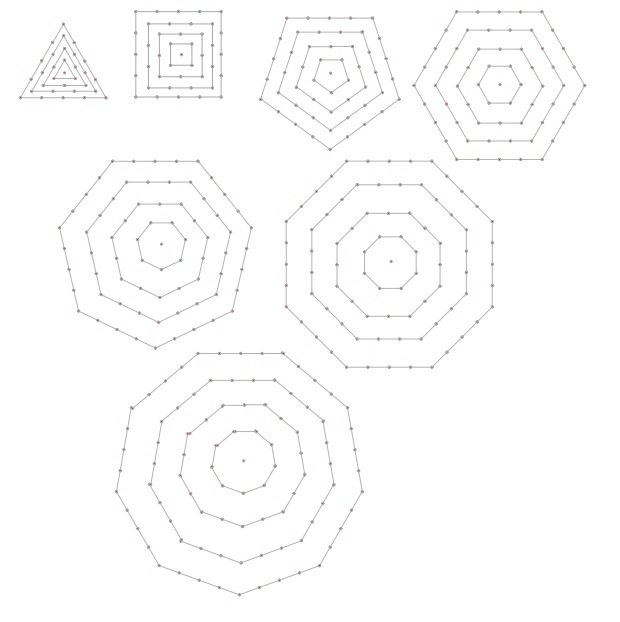
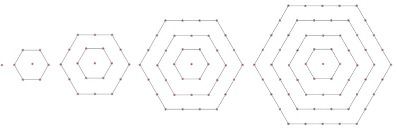
and for example, the centred hexagon numbers go $1, 7, 19, 37, 61$.

 

 Now it's over to you!

 
This investigation invites you to explore these sets of numbers and explore relationships within ordinary polygonal numbers and/or centred polygonal numbers.
You could also explore relationships between ordinary polygonal numbers and the centred polygonal numbers.
 
For example, you could explore which different polygonals (both centred and ordinary) have the same number occuring in the series?

KEY QUESTIONS:

What is the relationship between ordinary triangular polygonal numbers and others?

Can you re-arrange the dots from one polygonal to make another, and then generalise?
Throughout your exploration the question "Why?" probably needs to be asked!