Skip over navigation

Data Shapes

Age 5 to 7

Challenge Level Yellow star

Primary curriculum

Data Shapes

Sara and Will were sorting some pictures of shapes on cards.

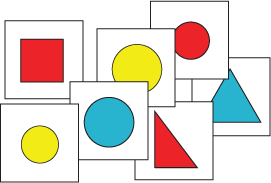
"I'll collect the circles," said Sara, "there are lots of those."
"I'll take the red ones," answered Will, "I like red."

Can you see any cards they would both want?

Here is a picture of all the cards they had.

How many cards could they have had each?

How many ways can you find to sort the cards?
Can you see any cards that are the same as other cards?

If you would like to make your own cards like these they can be downloaded here and cut into fifteen separate cards.

Why do this problem?

This problem uses simple shapes in three colours for sorting data in more than one way. Teachers and children may well think of other useful purposes for the cards.

If the shapes are printed onto thin card and laminated they should last a long time.

Possible approach

You could start by showing all the cards to the children and asking what they can tell you about them. This will be a good opportunity to listen to their use of mathematical vocabulary and introduce new terms where appropriate.

This problem is intended for children working in pairs, so that they are able to talk through their ideas with a partner. You could continue by giving each pair copies of these cards so that they can sort them in their own ways.

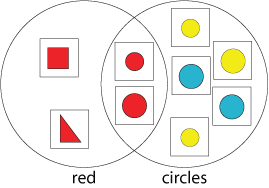
After they have had an opportunity to try sorting and to discuss with their partners how it could be done, it might be a good time to use, or introduce, a simple Venn diagram. This one shows how the question asked in the first part of the problem could be answered:

At the end of the lesson you could try different ways of sorting suggested by the children, using a Venn diagram if you think it appropriate.

Key questions

What can you see?

Can you think of another way you could sort the cards?

What is the same/different about these?

Tell me about what you are collecting.

Why do you think those two go together?

Where could you put this/these?

Possible extension

Learners could try one of the harder sorting problems, for example, Butterfly Cards.

Possible support

Some children may need a suggestion from you as to how to sort the cards to get them started.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Data Shapes

Data Shapes

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

Triangle Animals

Triple Cubes

The Add and Take-away Path