Hyperbolic Thinking

This problem naturally follows on from Trig Reps, although the two problems may be attempted independently.

Steve left the following cryptic page in his notebook:



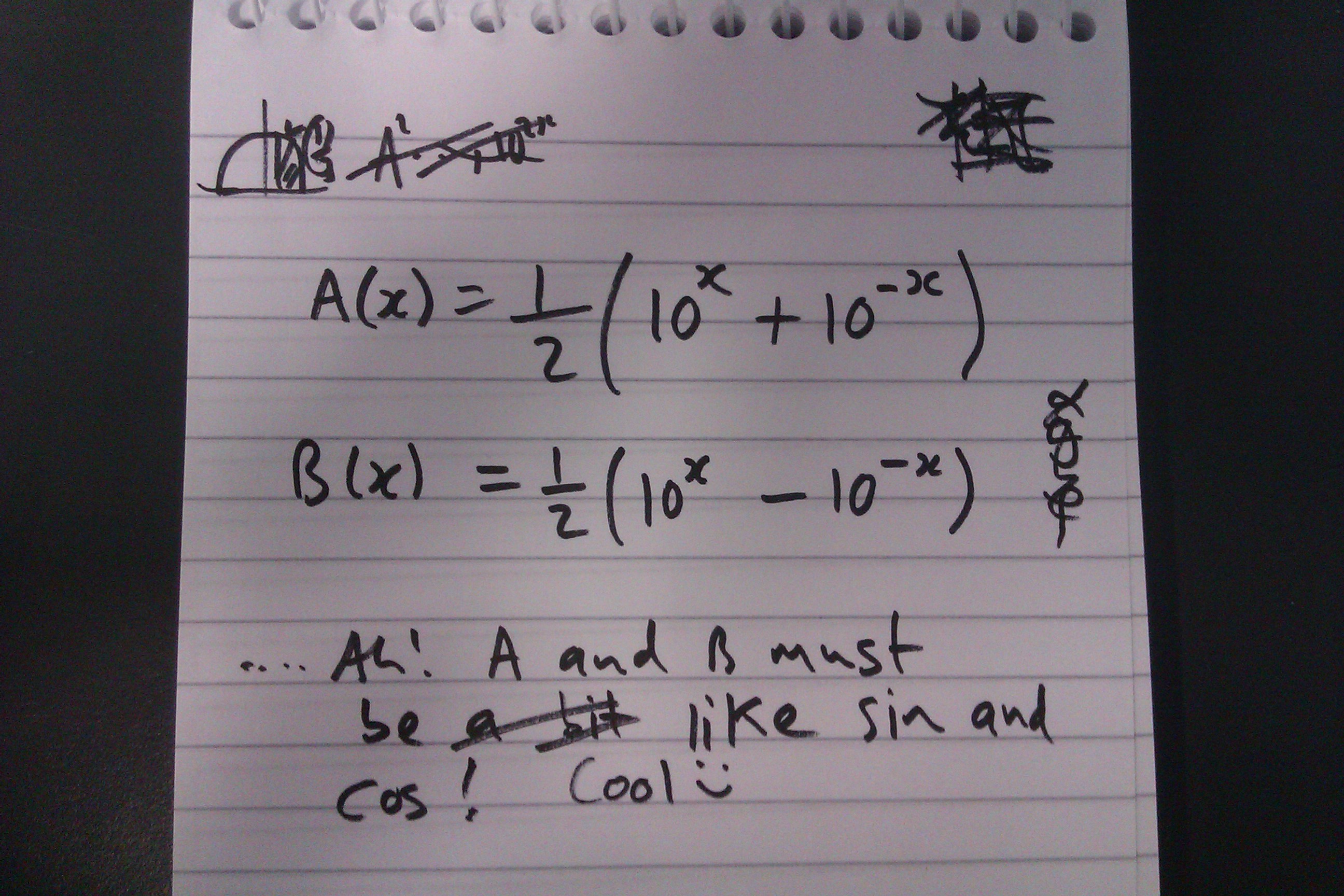
It seems that Steve thinks the following functions $A(x)$ and $B(x)$ are similar in some way to $\sin(x)$ and $\cos(x)$:

$$A(x) = \frac{1}{2}\Big(10^{x} +10^{-x}\Big)\quad\quad B(x) = \frac{1}{2}\Big(10^{x} -10^{-x}\Big)$$
Is Steve correct? To answer this question, think of as many properties of $\sin(x)$ and $\cos(x)$ as you can and, using these as a guide, explore the properties of $A(x)$ and $B(x)$.

Once you have done this you might wish to consider the properties of functions similar to $A(x)$ and $B(x)$ where the $10$ is replaced by different numbers. Do any of the properties hold for all of the bases? Which properties are base dependent? Is there a natural choice of base which the structure reveals?