Skip over navigation
Coordinate Geometry and Graphs
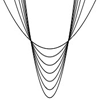
Parabolic Patterns
Age 14 to 18
Challenge Level 
The illustration shows the graphs of fifteen functions. Two of them have equations y=x^2 and y=-(x-4)^2. Find the equations of all the other graphs.
Parabella
Age 16 to 18
Challenge Level
This is a beautiful result involving a parabola and parallels.
Intersections
Age 14 to 18
Challenge Level
Change one equation in this pair of simultaneous equations very slightly and there is a big change in the solution. Why?
Tangled Trig Graphs
Age 16 to 18
Challenge Level
Can you work out the equations of the trig graphs I used to make my pattern?
Curve Match
Age 16 to 18
Challenge Level
Which curve is which, and how would you plan a route to pass between them?
Erratic Quadratic
Age 16 to 18
Challenge Level
Can you find a quadratic equation which passes close to these points?
Whose Line Graph Is it Anyway?
Age 16 to 18
Challenge Level
Which line graph, equations and physical processes go together?