Skip over navigation
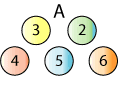
The numbers on the balls are added together: $4 + 5 = 9$
If the total is even, you win.
If the total is odd, you lose.
How can you decide whether the game is fair?
You might like to experiment with the interactivity below.
Here are three more sets of balls:
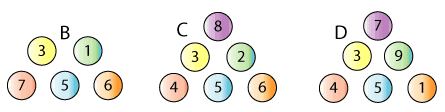
Which set would you choose to play with, to maximise your chances of winning?
Click on the links below to explore each set using the interactivity.
What proportion of the time would you expect to win each game?
You may wish to look at the problem Odds and Evens Made Fair to explore whether it is possible to change the number of balls to make the game fair.
Odds and Evens
Age 11 to 14
Challenge Level 
Odds and Evens printable sheet
Here is a set of numbered balls used for a game:
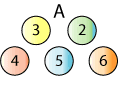
To play the game, the balls are mixed up and two balls are randomly picked out together. For example:
The numbers on the balls are added together: $4 + 5 = 9$
If the total is even, you win.
If the total is odd, you lose.
How can you decide whether the game is fair?
You might like to experiment with the interactivity below.
Here are three more sets of balls:
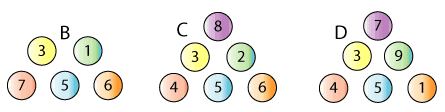
Which set would you choose to play with, to maximise your chances of winning?
Click on the links below to explore each set using the interactivity.
What proportion of the time would you expect to win each game?
You may wish to look at the problem Odds and Evens Made Fair to explore whether it is possible to change the number of balls to make the game fair.
You may also like
Stop or Dare
All you need for this game is a pack of cards. While you play the game, think about strategies that will increase your chances of winning.
Snail Trails
This is a game for two players. Does it matter where the target is put? Is there a good strategy for winning?
Game of PIG - Sixes
Can you beat Piggy in this simple dice game? Can you figure out Piggy's strategy, and is there a better one?