Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Polygon Rings



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem starts with the context of regular polygons and poses a question that will lead students on an exploration involving angles, factors, multiples and constructions. The interactive environment provides a playground for students' curiosity, and allows them to generate lots of examples in order to notice patterns, make predictions, and prove their conjectures.
You can read more about the use of digital manipulatives in the article that accompanies this feature.
Possible approach
As well as using the interactivity, you might wish to use physical tiles to investigate this problem. The Association of Teachers of Mathematics sell a range of ATM MATs which could be used. Alternatively, there are some pages of shapes that can be printed out on our Semi-regular Tessellations page.
Show the image from the problem:
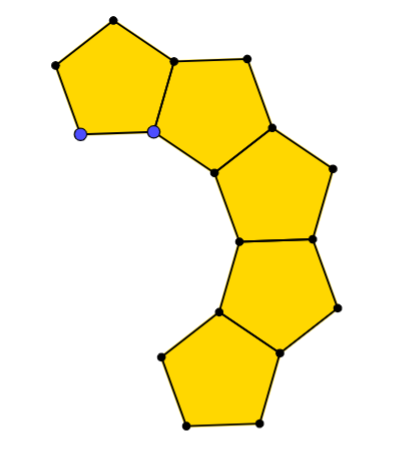
"Here is a pattern made from regular pentagons. What do you think will happen if we continue to add pentagons?"
Some students might predict that 10 will form a closed loop, others might think it will not line up or that it will overlap. Take some time to discuss their ideas, focussing on vocabulary such as symmetry, parallel lines, and angles. Then resolve the discussion using the interactivity in the problem, showing that 10 regular pentagons form a closed loop with a regular decagon inside.
"How can we be sure that it's actually a closed loop and not just very close?" Students might need reminding how to find the interior angles of regular polygons, and then perhaps the class could work together on a proof that the angle between the two pentagons is in fact the interior angle of a regular decagon: $108^{\circ} + 108^{\circ}+ 144^{\circ} = 360^{\circ}$.
Students could then go on to explore polygon rings with other shapes. If laptops or tablets are available, they could create diagrams using the interactivity.
After students have worked with other shapes, you could collect together their findings in a table on the board:
| Shape | Number needed to form a ring |
| Pentagon | 10 |
| Hexagon | 6 (or 3, for a ring without a hole in the middle!) |
| Heptagon | 14 |
| Octagon | 4 or 8 |
This could lead students to explore the following key questions:
Can you make a ring with any regular polygon?
Is there a way to predict how many n-sided polygons you need to form a ring?
Possible support
Encourage students to create a polygon ring using the interactivity, and then take a screenshot to print out a large version. Then they can annotate the diagram with the angles that they know, and use it to work out other angles.
Possible extension
Students could prove what would happen with polygons with too many sides to draw using the interactivity.
Students could also explore rings made from more than one type of regular polygon, like these ones:
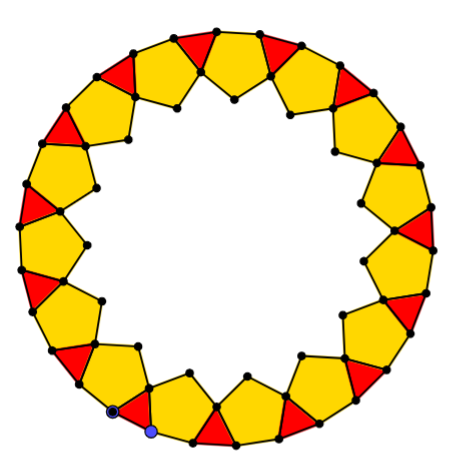
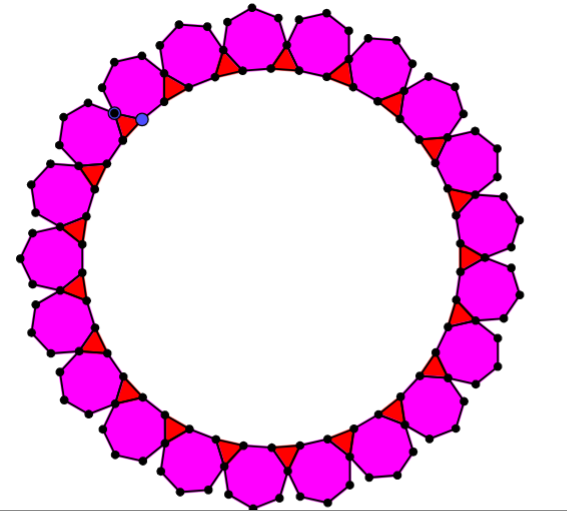
Semi-regular Tessellations and Which Solids Can We Make? could be explored next.
You may also like
Arclets Explained
This article gives an wonderful insight into students working on the Arclets problem that first appeared in the Sept 2002 edition of the NRICH website.
Bow Tie
Show how this pentagonal tile can be used to tile the plane and describe the transformations which map this pentagon to its images in the tiling.

