Tilted Squares

Age 11 to 14

Challenge Level Yellow star

Why do this problem?

This problem offers an opportunity to spot patterns, make generalisations and eventually discover Pythagoras's Theorem, while giving students the chance to practise working out areas of squares and right-angled triangles.

Possible approach

This printable worksheet may be useful: Tilted Squares.

The video below shows Charlie and Alison from the NRICH team introducing the problem to a group of Year 9 students who came to visit the Maths Department at Cambridge. Video footage of the later stages of the lesson appear further down the page.

Video 1

Here is a description based on the approach used by a teacher with a Year 8 class, interspersed with some more video footage from the lesson in Cambridge:

I established that everyone could work out the area of squares when they were in the usual orientation:

"4 by 4?"

"16"

"5 by 5?"

"25"

etc.

"But what if we had to work out the area of a tilted square?"

I drew a point on the board, then moved 3 units to the right and 1 unit up and drew another point there.

I used this as the base of my square and then drew the other three sides.

The interactivity in this task could be used to familiarise students with drawing tilted squares.

"How might we work out the area of this square?"

One student suggested that the base was 3 cm long and that the area would be $\text{9 cm}^2$.

One student suggested we measure the length with a ruler and then square the result.

We discussed the problems with the two approaches and then I drew a 4 by 4 square around the tilted square and suggested that if we boxed the square in, worked out the area of the box (16 cm$^2$) and subtracted the area of the four unwanted triangles (6 cm$^2$) we would have the area of our tilted square (10 cm$^2$). See the hint for a diagram and an alternative method.

"It would be nice to be able to work out the areas of these tilted squares as fast as you worked out the areas of the original squares"

Students in one row were asked to draw a square with a base that went 4 along and 1 up.

Students in the next row were asked to draw a square with a base that went 5 along and 1 up.

Students in the next row were asked to draw a square with a base that went 6 along and 1 up. Students in the next row were asked to draw a square with a base that went 7 along and 1 up.

Here is a second video clip, showing the results being collected (approximately 5 minutes later) in the lesson in Cambridge:

Video 2

Students were all asked to work out the area of their squares and I then collected their results:

4 along and 1 up: 17

5 along and 1 up: 26

6 along and 1 up: 37

7 along and 1 up: 50

"Do you notice anything about the areas?"

"All 1 more than a square number"

"If you drew a square with a base 8 along and 1 up, what would you expect the area to be?"

"65"

"If you drew a square with a base x along and 1 up, what would you expect the area to be?"

"x$^2$ + 1"

"Great, it looks like we can now work out the areas of these tilted squares very easily."

But what would happen if they were more tilted, say, 3 along and 2 up, or 4 along and 2 up, or...?"

Someone suggested that the rule would be x$^2$ + 2

Here is the final video clip, showing the last part of the lesson in Cambridge, when students made the generalisation that leads to Pythagoras's Theorem:

Video 3

Again the class was split up to work out the areas of these tilted squares and we then collected their results:

3 along and 2 up: 13

4 along and 2 up: 20

5 along and 2 up: 29

6 along and 2 up: 40

"Was our conjecture (x$^2$ + 2) correct?"

"It's x$^2$ + 4"

"It's x$^2$ + 2$^2$"

"The first one should have been x$^2$ + 1$^2$"

At this point, it may be appropriate to work on some ways of justifying the $x^2 + 1^2$ and $x^2 + 2^2$ conjectures.

For groups who have met the idea of expanding $(x+1)^2$ this can be done algebraically.

Alternatively, a pictorial approach could be offered, and students could be asked to explain why this proves their conjecture:

"What do you think will happen if the squares are even more tilted, say 3, or 4, or 5 up?"

"x$^2$ + 3$^2$"

"x$^2$ + 4$^2$"

"x$^2$ + 5$^2$"

Students were split into groups again in the following lesson to check these conjectures and report back.

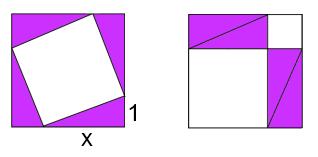
Finally, algebraic or pictorial approaches used to justify earlier conjectures can be adapted to prove Pythagoras's Theorem:

An 'x across, 1 up' tilted square can be enclosed by a square of side length x + 1. The area
of the tilted square is $(x + 1)^2$ minus the areas of the four unwanted triangles. This equals
$(x^2 + 2x + 1) - 2x = x^2 + 1$, as predicted.

An 'x across, 2 up' tilted square can be enclosed by a square of side length x + 2. The area of the tilted square is $(x + 2)^2$ minus the areas of the four unwanted triangles. This equals
$(x^2 + 4x + 4) - 4x = x^2 + 4$, as predicted.

An 'x across, y up' tilted square can be enclosed by a square of side length x + y. The area of the tilted square is $(x + y)^2$ minus the areas of the four unwanted triangles. This equals $(x^2 + 2xy + y^2) - 2xy = x^2 + y^2$, as predicted.

Follow-up lessons could focus on working out the lengths of the sides of right-angled triangles when two lengths have been given.

Key questions

How could you work out the area of a tilted square?

If you drew a square with a base x along and 1 up, what would you expect the area to be?

If you drew a square with a base x along and 2 up, what would you expect the area to be?

If you drew a square with a base x along and y up, what would you expect the area to be?

Possible support

Start with Square It or Square Coordinates to help students become confident at drawing tilted squares.

Possible extension

It is possible to draw squares with areas of 1, 2, 4, 5, 8, 9... but not 3, 6, 7, 11, 12...

Students could explore some of the properties of numbers which are and are not possible areas of tilted squares.

Can they prove that numbers of the form 4n+3 are not possible areas of tilted squares?

Another possible follow-up task is Of All the Areas.

NOTES AND BACKGROUND Ken Nisbet, Mathematics teacher at Madras College in Fife, Scotland, has added:

"I used tilted squares as the basis of individual/group work with a top set (age 14). They were given time to explore this as an open ended question in groups in a brain storming session. Write ups were to be done individually, partly in class but completed at home. This is an important stage in the pupils' mathematical development where the idea of "proof" is coming to the fore. This excellent investigation allows algebra to come to the fore as the language of generalisation and the means of "proof" of patterns. At this stage algebra skills are limited but we have now used this investigation as a springboard to developing necessary algebra skills - e.g. double brackets, squares, expressions etc."

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Tilted Squares

Why do this problem?

Possible approach

Key questions

Possible support

Possible extension

You may also like

Have You Got It?

Counting Factors

Is There a Theorem?