Tilted Squares

Pavamaan, Vedant, Asad and Shreyash from Wilson's Grammar School and Lydia from Hymers College, all in the UK, explained how to find the area of a tilted square. This is the beginning of Lydia's explanation:

For squares with a tilt of one, draw a square around it that is oriented in the usual way. The square must touch all the corners of the tilted square.

Asad's diagram shows what to do next:

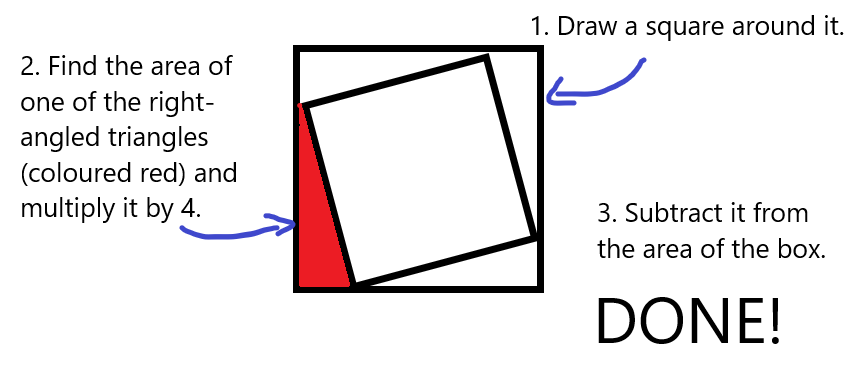
Pavamaan also explained how to work out the area of the red triangle:

To find the area of one of the right-angled triangles, what you have to do is you have to form a rectangle, or a square if the tilted square is tilted by 2, by drawing the the same right-angled triangle again but the other way underneath that triangle; this makes a rectangle. This rectangle is not tilted but straight, which makes it easy to work out the area from. So find the area of the rectangle and then half that rectangle area to find the area of the right-angled triangle.

Johnny from Trinity School and Alex from Long Field Academy Melton Mowbray investigated different tilts. They both made the same conjecture. This is Johnny's work:

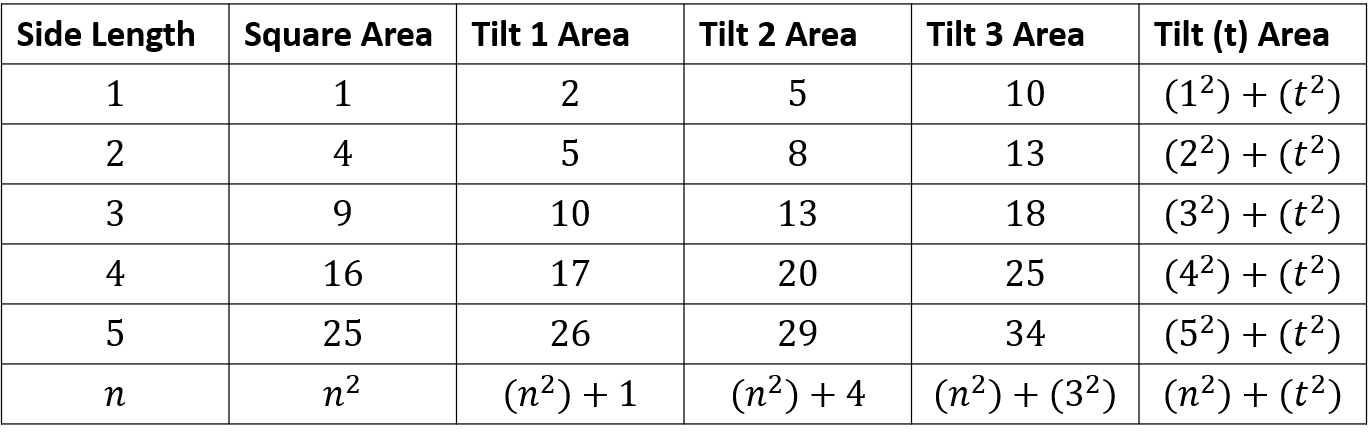
Rule: Tilt area = square area + (tilt)$^2$, or $n^2 + t^2$ where $n = $ square length and $t = $ tilt of square

Alex used a diagram to prove the rule: