Skip over navigation
Hannah from Munich International School worked out which numbers between 1 and 30 were possible:
1: $1^2 - 0^2$ is $1 - 0 = 1$
2: does not work
3: $2^2 - 1^2$ is $4 - 1 = 3$
4: $2^2 - 0^2$ is $4 - 0 = 4$
5: $3^2 - 2^2$ is $9 - 4 = 5$
6: does not work
7: $4^2 - 3^2$ is $16 - 9 = 7$
8: $3^2 - 1^2$ is $9 - 1 = 8$
9: $5^2 - 4^2$ is $25 - 16 = 9$
10: does not work
11: $6^2 - 5^2$ is $36 - 25 = 11$
12: $4^2 - 2^2$ is $16 - 4 = 12$
13: $7^2 - 6^2$ is $49 - 36 = 13$
14: does not work
15: $8^2 - 7^2$ is $64 - 49 = 15$
16: $5^2 - 3^2$ is $25 - 9 = 16$
17: $9^2 - 8^2$ is $81 - 64 = 17$
18: does not work
19: $10^2 - 9^2$ is $100 - 81 = 19$
20: $6^2 - 4^2$ is $36 - 16 = 20$
21: $11^2 - 10^2$ is $121-100 = 21$
22: does not work
23: $12^2 - 11^2$ is $144-121=23$
24: $7^2-5^2$ is $49 - 25 = 24$
25: $13^2 - 12^2$ is $169-144=25$
26: does not work
27: $14^2 - 13^2$ is $196 - 169 = 27$
28: $8^2 - 6^2$ is $64-36 = 28$
29: $15^2 - 14^2$ is $225 - 196 = 29$
30: does not work
You can express 22 of the 30 numbers as a difference of two perfect squares. A pattern occuring throughout these solutions is that all odd numbers can be represented by a difference of two perfect squares, as well as all numbers resulting in an integer when divided by four.
Joshua from St John's School used algebra to show how odd numbers and multiples of four could be made:
You can make every odd number by taking consecutive squares.
$(n+1)^2 - n^2 = 2n+1$, every odd number can be written in the form $2n+1$.
Similarly, you can make every multiple of 4 by taking squares with a difference of 2.
All other numbers you can't make:
$(n+x)^2 - n^2 = x^2 + 2nx = x(x+2n)$
If $x$ is odd then $x^2$ is also odd and $2nx$ is even. An odd plus an even is odd.
If $x$ is even then $x^2$ is a multiple of $4$ and $2nx$ is also a multiple of $4$ so $(n+x)^2 - n^2$ is a multiple of $4$.
Numbers such as 2,6,10 etc can't be made because these are made by multiplying an even by an odd.
Patrick from Woodbridge School and Richard from Mearns Castle School both used a formula for the difference of two squares to investigate which numbers were possible. Here is Patrick's solution:
$a^2 - b^2= (a + b)(a - b)$
Thus, a number $n$ can only be a difference of two squares if it has two factors of the form $(a + b)$ and $(a - b)$, where $a + b \geq \sqrt{n}$ and $a - b \leq \sqrt{n}$.
If $1$ could be written as the difference of squares then $(a + b) = (a - b) = 1$, as the only factor of $1$ is $1$.
Thus, $a = 1$ and $b = 0$. So $1 = 1^2 - 0^2$.
If $2$ could be written as the difference of two squares then $(a + b) = 2$ and $(a - b) = 1$, as $2$ is prime, and clearly $a - b < a + b$ for positive $b$.
Thus, solving the simultaneous equations, $b = 2 - a$, so $a - (2 - a) = 1$, $2a = 3$ and $a = \frac{3}{2}$. Thus, $2$ is not representable as the difference of two integer squares.
This method can be generalised for any prime $p$ by solving $(a + b) = p$ and $(a - b) = 1$
Adding the equations gives $2a = p + 1$, so $a = \frac{p+1}{2}$. Since $a - b = 1$, $b = a-1$, so $b = \frac{p+1}{2} - 1 = \frac{p-1}{2}$. Thus, any odd prime can be written as the difference of two squares.
Any square number $n$ can also be written as the difference of two squares, by taking $a = \sqrt{n}$ and $b = 0$.
Generally, a number can be written as the difference of two squares if it has two factors of the same parity, since if $a + b$ is odd and $a - b$ is even, when the two equations are added we would get $2a$ odd, so the solution would not be an integer. So a number cannot be written as a difference of two squares if and only if it is equivalent to $2$ mod $4$ (leaves a remainder of $2$ when divided by $4$).
Richard from Comberton Village College considered prime factorisation:
An integer $x$ can be written as the difference between two square integers unless it contains only one $2$ in its prime power factorisation.
Proof: $x=a^2 - b^2$ can be rewritten in the form $(a+b)(a-b)$.
Suppose $u$ and $v$ are two factors of $x$ such that $u = a + b$ and $v = a - b$.
Subtracting the two equations, we get $u - v = 2b$.
This tells us that the difference between the two factors will always be even if the number can be written in this form.
Now, to get an even difference, we either need $u$ and $v$ to be both odd, or both even. Therefore, any number with either two even or odd factors can be written in this form.
This leaves numbers which will always have one odd and one even factor.
If $v$ is an odd factor of $x$, it must have a prime factorisation of only odd numbers.
Suppose $u$ is an even factor of $x$ and contains more than one $2$ in its prime factorisation.
This means that $u$ could be divided by two and still be even, and at the same time $v$ could be doubled so that it too is even. This means that $x$ has a factor pair which are both even, and so can be written as the difference of two squares.
If both factors are odd an even difference will also be attained, so if there are no twos in the prime factorisation of $x$, then x can be written as the difference of two squares.
This leaves the case where there is exactly one $2$ in the prime factorisation. This means that one factor must contain the $2$ and not the other, and that the factors cannot be manipulated in the fashion described before. This will always leave factors with an odd difference suggesting $x$ cannot be written as the difference of two squares.
This also gives a very nice algorithm for finding two squares which have a difference of $x$:
1. Establish how many $2$s are in the prime factorisation of $x$. If there is only one, x cannot be written as the difference of two squares.
2. Choose a factor pair which are both even or both odd, call them $u$ and $v$. Find their difference and divide it by 2 to find the smaller square. $\frac{u - v}{2}=b$ from before.
3. Square $b$ and add it to $x$. Square root the sum and that is $a$.
We now have $x = a^2 - b^2$.
For example, $60 = 2 \times 2 \times 3 \times 5$. There is more than one 2 so it is possible.
The two factors $2 \times 5 = 10$ and $2 \times 3 = 6$ give a difference of 4. Halve it to get $b = 2$.
$x + b^2 = 60 + 4 = 64$. $\sqrt{64} = 8$, so $a = 8$.
This gives us $60 = 8^2 - 2^2$.
We could also have taken $u = 2 \times 3 \times 5$ and $v = 2$, which gives a difference of 28. Halve it to get $b=14$.
$x + b^2 = 60 + 196 = 256$.
$\sqrt{256} = 16$ so $a = 16$.
$16^2 - 14^2 = 60$

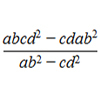

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
What's Possible?
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Hannah from Munich International School worked out which numbers between 1 and 30 were possible:
1: $1^2 - 0^2$ is $1 - 0 = 1$
2: does not work
3: $2^2 - 1^2$ is $4 - 1 = 3$
4: $2^2 - 0^2$ is $4 - 0 = 4$
5: $3^2 - 2^2$ is $9 - 4 = 5$
6: does not work
7: $4^2 - 3^2$ is $16 - 9 = 7$
8: $3^2 - 1^2$ is $9 - 1 = 8$
9: $5^2 - 4^2$ is $25 - 16 = 9$
10: does not work
11: $6^2 - 5^2$ is $36 - 25 = 11$
12: $4^2 - 2^2$ is $16 - 4 = 12$
13: $7^2 - 6^2$ is $49 - 36 = 13$
14: does not work
15: $8^2 - 7^2$ is $64 - 49 = 15$
16: $5^2 - 3^2$ is $25 - 9 = 16$
17: $9^2 - 8^2$ is $81 - 64 = 17$
18: does not work
19: $10^2 - 9^2$ is $100 - 81 = 19$
20: $6^2 - 4^2$ is $36 - 16 = 20$
21: $11^2 - 10^2$ is $121-100 = 21$
22: does not work
23: $12^2 - 11^2$ is $144-121=23$
24: $7^2-5^2$ is $49 - 25 = 24$
25: $13^2 - 12^2$ is $169-144=25$
26: does not work
27: $14^2 - 13^2$ is $196 - 169 = 27$
28: $8^2 - 6^2$ is $64-36 = 28$
29: $15^2 - 14^2$ is $225 - 196 = 29$
30: does not work
You can express 22 of the 30 numbers as a difference of two perfect squares. A pattern occuring throughout these solutions is that all odd numbers can be represented by a difference of two perfect squares, as well as all numbers resulting in an integer when divided by four.
Joshua from St John's School used algebra to show how odd numbers and multiples of four could be made:
You can make every odd number by taking consecutive squares.
$(n+1)^2 - n^2 = 2n+1$, every odd number can be written in the form $2n+1$.
Similarly, you can make every multiple of 4 by taking squares with a difference of 2.
All other numbers you can't make:
$(n+x)^2 - n^2 = x^2 + 2nx = x(x+2n)$
If $x$ is odd then $x^2$ is also odd and $2nx$ is even. An odd plus an even is odd.
If $x$ is even then $x^2$ is a multiple of $4$ and $2nx$ is also a multiple of $4$ so $(n+x)^2 - n^2$ is a multiple of $4$.
Numbers such as 2,6,10 etc can't be made because these are made by multiplying an even by an odd.
Patrick from Woodbridge School and Richard from Mearns Castle School both used a formula for the difference of two squares to investigate which numbers were possible. Here is Patrick's solution:
$a^2 - b^2= (a + b)(a - b)$
Thus, a number $n$ can only be a difference of two squares if it has two factors of the form $(a + b)$ and $(a - b)$, where $a + b \geq \sqrt{n}$ and $a - b \leq \sqrt{n}$.
If $1$ could be written as the difference of squares then $(a + b) = (a - b) = 1$, as the only factor of $1$ is $1$.
Thus, $a = 1$ and $b = 0$. So $1 = 1^2 - 0^2$.
If $2$ could be written as the difference of two squares then $(a + b) = 2$ and $(a - b) = 1$, as $2$ is prime, and clearly $a - b < a + b$ for positive $b$.
Thus, solving the simultaneous equations, $b = 2 - a$, so $a - (2 - a) = 1$, $2a = 3$ and $a = \frac{3}{2}$. Thus, $2$ is not representable as the difference of two integer squares.
This method can be generalised for any prime $p$ by solving $(a + b) = p$ and $(a - b) = 1$
Adding the equations gives $2a = p + 1$, so $a = \frac{p+1}{2}$. Since $a - b = 1$, $b = a-1$, so $b = \frac{p+1}{2} - 1 = \frac{p-1}{2}$. Thus, any odd prime can be written as the difference of two squares.
Any square number $n$ can also be written as the difference of two squares, by taking $a = \sqrt{n}$ and $b = 0$.
Generally, a number can be written as the difference of two squares if it has two factors of the same parity, since if $a + b$ is odd and $a - b$ is even, when the two equations are added we would get $2a$ odd, so the solution would not be an integer. So a number cannot be written as a difference of two squares if and only if it is equivalent to $2$ mod $4$ (leaves a remainder of $2$ when divided by $4$).
Richard from Comberton Village College considered prime factorisation:
An integer $x$ can be written as the difference between two square integers unless it contains only one $2$ in its prime power factorisation.
Proof: $x=a^2 - b^2$ can be rewritten in the form $(a+b)(a-b)$.
Suppose $u$ and $v$ are two factors of $x$ such that $u = a + b$ and $v = a - b$.
Subtracting the two equations, we get $u - v = 2b$.
This tells us that the difference between the two factors will always be even if the number can be written in this form.
Now, to get an even difference, we either need $u$ and $v$ to be both odd, or both even. Therefore, any number with either two even or odd factors can be written in this form.
This leaves numbers which will always have one odd and one even factor.
If $v$ is an odd factor of $x$, it must have a prime factorisation of only odd numbers.
Suppose $u$ is an even factor of $x$ and contains more than one $2$ in its prime factorisation.
This means that $u$ could be divided by two and still be even, and at the same time $v$ could be doubled so that it too is even. This means that $x$ has a factor pair which are both even, and so can be written as the difference of two squares.
If both factors are odd an even difference will also be attained, so if there are no twos in the prime factorisation of $x$, then x can be written as the difference of two squares.
This leaves the case where there is exactly one $2$ in the prime factorisation. This means that one factor must contain the $2$ and not the other, and that the factors cannot be manipulated in the fashion described before. This will always leave factors with an odd difference suggesting $x$ cannot be written as the difference of two squares.
This also gives a very nice algorithm for finding two squares which have a difference of $x$:
1. Establish how many $2$s are in the prime factorisation of $x$. If there is only one, x cannot be written as the difference of two squares.
2. Choose a factor pair which are both even or both odd, call them $u$ and $v$. Find their difference and divide it by 2 to find the smaller square. $\frac{u - v}{2}=b$ from before.
3. Square $b$ and add it to $x$. Square root the sum and that is $a$.
We now have $x = a^2 - b^2$.
For example, $60 = 2 \times 2 \times 3 \times 5$. There is more than one 2 so it is possible.
The two factors $2 \times 5 = 10$ and $2 \times 3 = 6$ give a difference of 4. Halve it to get $b = 2$.
$x + b^2 = 60 + 4 = 64$. $\sqrt{64} = 8$, so $a = 8$.
This gives us $60 = 8^2 - 2^2$.
We could also have taken $u = 2 \times 3 \times 5$ and $v = 2$, which gives a difference of 28. Halve it to get $b=14$.
$x + b^2 = 60 + 196 = 256$.
$\sqrt{256} = 16$ so $a = 16$.
$16^2 - 14^2 = 60$
Related Collections
You may also like
Euler's Squares
Euler found four whole numbers such that the sum of any two of the numbers is a perfect square...
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
2-digit Square
A 2-Digit number is squared. When this 2-digit number is reversed and squared, the difference between the squares is also a square. What is the 2-digit number?

