Skip over navigation
Thank you and well done to everyone who submitted solutions to this problem. There were lots and lots of correct solutions, so we couldn't mention you all. In fact, choosing between them was difficult!
Problem 1
Harry and Jack, from Chew Valley School, sent this solution:
$10A+B=(A+B)\times4$, because $A$ has to be multiplied by ten to make it a 2 digit number.
$10A+B=4A+4B$, because you multiply out of the brackets and are left with this.
$10A-4A=4B-B$
So $6A=3B$
So $2A=B$
In other words, the units have to be double the tens, so the numbers are $12$, $24$, $36$ and $48$.
Problem 2
Tim, from Gosforth Academy, sent this solution:
$ABC + AB + C = 100A + 10B + C + 10A + B + C = 300$
$110A + 11B + 2C = 300$
A has to be below $3$, because $110 \times 3$ gives $330$, which is greater than $300$.
However, it can't be $1$, because that would leave $11B + 2C$ equalling $190$, and with the maximum value of 9, this clearly cannot be true: $(11 \times 9) + (2 \times 9) = 117$.
Therefore, $A = 2$.
Substitute this in and we get:
$(2 \times 110) + 11B + 2C = 300$
$11B + 2C =80$
The maximum value of $2C$ is $2 \times 9 = 18$, so the minimum value of $11B$ is $80 - 18 = 62$.
Of course, $11B$ must be a multiple of $11$, and it also has to be even, because $2C$ and $80$ are both even. The only even multiple of $11$ between $62$ and $80$ is $66$, which must equal 11B, so B = 6.
Substituting this into the equation gives:
$(11 \times 6) + 2C = 80$
$2C = 14$
$C = 7$
So we have only one possible set of values: $A = 2$, $B = 6$ and $C = 7$
To check this, $267 + 26 + 7$ does equal $300$.
Problem 3
Zainab, Amy, Ellie, from Sandbach High School, sent this solution:
Choose a two-digit number with two different digits ($AB$) and form itsreversal (i.e. $BA$).
$AB$ and $BA$ are $10A+B$ and $10B+A$
Subtracting $(A+B)$ gives $9A$ and $9B$.
Adding these gives $9A+9B=9(A+B)$, a multiple of 9.
Problem 4
Emma, from Sandbach High School, sent this solution:
The 6 numbers are:
$10A+B$
$10B+C$
$10C+A$
$10A+C$
$10B+A$
$10C+B$
The total is $22A+22B+22C =22(A+B+C)$. Dividing by $A+B+C$ gives $22$.
Problem 5
Julian, from the British School, Manila, in the Philippines, sent this solution:
Since $a>b>c$, to make the differences non-negative the differences will be:
$(10a+b)-(10b+a)$, $(10b+c)-(10c+b)$, and $(10a+c)-(10c+a)$
These are $9a-9b$, $9b-9c$, and $9a-9c$.
When you add these results you get $18a-18c=18(a-c)$ which is clearly divisible by $18$.
Problem 6
Zach sent us this this solution:
$100A+10B+C=(10A+B)+(10B+C)+(10C+A)$
Simplifying gives:
$100A+10B+C=11A+11B+11C$
$89A = 10C+B$
Since we can only use the digits $1$ to $9$, the only possible solution for $A$ is $A=1$, because any larger $A$ gives a $3$ digit number.
This leaves $C=8$ and $B=9$.
To check, $19+98+81=198$.
Problem 7
Sergio, from the King's College of Alicante, Spain, sent this solution:
Firstly I transformed it into an equation: $10a+b+10c+d=10d+c+10b+a$.
This simplifies to $9a-9b+9c-9d=0$, and dividing by $9$ gives $a+c=b+d$.
This will always work because the first equation is the same as the last one, just in a simplified form, and you could undo all of the steps.
It is like the quadratic equation, $ax^2+bx+c$ is the same as the quadratic formula, just that it ´s rearranged to make $x$ the subject. Well here it ´s the same but putting each letter only once.
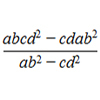

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Puzzling Place Value
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
Thank you and well done to everyone who submitted solutions to this problem. There were lots and lots of correct solutions, so we couldn't mention you all. In fact, choosing between them was difficult!
Problem 1
Harry and Jack, from Chew Valley School, sent this solution:
$10A+B=(A+B)\times4$, because $A$ has to be multiplied by ten to make it a 2 digit number.
$10A+B=4A+4B$, because you multiply out of the brackets and are left with this.
$10A-4A=4B-B$
So $6A=3B$
So $2A=B$
In other words, the units have to be double the tens, so the numbers are $12$, $24$, $36$ and $48$.
Problem 2
Tim, from Gosforth Academy, sent this solution:
$ABC + AB + C = 100A + 10B + C + 10A + B + C = 300$
$110A + 11B + 2C = 300$
A has to be below $3$, because $110 \times 3$ gives $330$, which is greater than $300$.
However, it can't be $1$, because that would leave $11B + 2C$ equalling $190$, and with the maximum value of 9, this clearly cannot be true: $(11 \times 9) + (2 \times 9) = 117$.
Therefore, $A = 2$.
Substitute this in and we get:
$(2 \times 110) + 11B + 2C = 300$
$11B + 2C =80$
The maximum value of $2C$ is $2 \times 9 = 18$, so the minimum value of $11B$ is $80 - 18 = 62$.
Of course, $11B$ must be a multiple of $11$, and it also has to be even, because $2C$ and $80$ are both even. The only even multiple of $11$ between $62$ and $80$ is $66$, which must equal 11B, so B = 6.
Substituting this into the equation gives:
$(11 \times 6) + 2C = 80$
$2C = 14$
$C = 7$
So we have only one possible set of values: $A = 2$, $B = 6$ and $C = 7$
To check this, $267 + 26 + 7$ does equal $300$.
Problem 3
Zainab, Amy, Ellie, from Sandbach High School, sent this solution:
Choose a two-digit number with two different digits ($AB$) and form itsreversal (i.e. $BA$).
$AB$ and $BA$ are $10A+B$ and $10B+A$
Subtracting $(A+B)$ gives $9A$ and $9B$.
Adding these gives $9A+9B=9(A+B)$, a multiple of 9.
Problem 4
Emma, from Sandbach High School, sent this solution:
The 6 numbers are:
$10A+B$
$10B+C$
$10C+A$
$10A+C$
$10B+A$
$10C+B$
The total is $22A+22B+22C =22(A+B+C)$. Dividing by $A+B+C$ gives $22$.
Problem 5
Julian, from the British School, Manila, in the Philippines, sent this solution:
Since $a>b>c$, to make the differences non-negative the differences will be:
$(10a+b)-(10b+a)$, $(10b+c)-(10c+b)$, and $(10a+c)-(10c+a)$
These are $9a-9b$, $9b-9c$, and $9a-9c$.
When you add these results you get $18a-18c=18(a-c)$ which is clearly divisible by $18$.
Problem 6
Zach sent us this this solution:
$100A+10B+C=(10A+B)+(10B+C)+(10C+A)$
Simplifying gives:
$100A+10B+C=11A+11B+11C$
$89A = 10C+B$
Since we can only use the digits $1$ to $9$, the only possible solution for $A$ is $A=1$, because any larger $A$ gives a $3$ digit number.
This leaves $C=8$ and $B=9$.
To check, $19+98+81=198$.
Problem 7
Sergio, from the King's College of Alicante, Spain, sent this solution:
Firstly I transformed it into an equation: $10a+b+10c+d=10d+c+10b+a$.
This simplifies to $9a-9b+9c-9d=0$, and dividing by $9$ gives $a+c=b+d$.
This will always work because the first equation is the same as the last one, just in a simplified form, and you could undo all of the steps.
It is like the quadratic equation, $ax^2+bx+c$ is the same as the quadratic formula, just that it ´s rearranged to make $x$ the subject. Well here it ´s the same but putting each letter only once.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.

