Sliding Rectangles
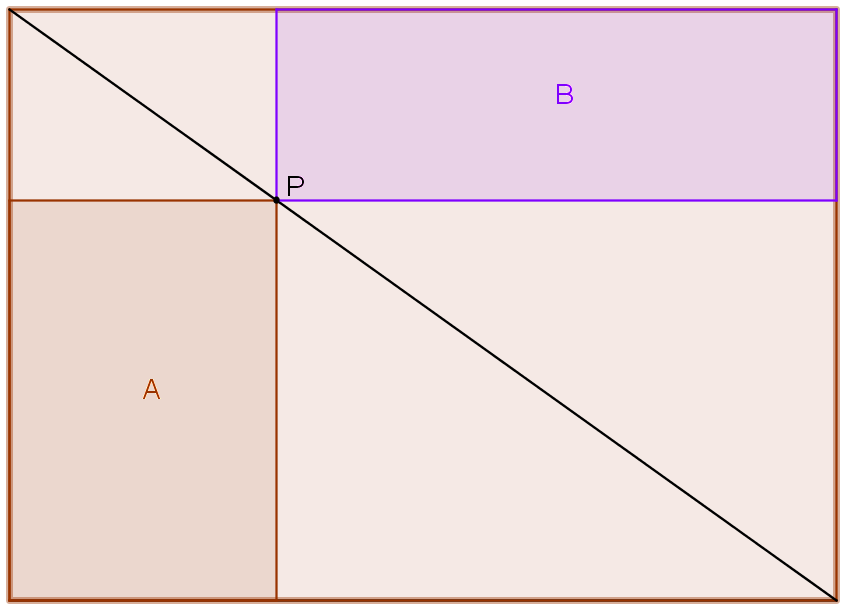
The picture to the right shows a rectangle with a diagonal drawn on it.
An arbitrary point, $P$, has been placed on the diagonal.
The two shaded rectangles, $A$ and $B$, have a common vertex at $P$.
Which of these two rectangles has the greater area?
Below is an interactive version of the picture above. You may find it helpful to click and drag point $P$, and see how the two rectangles $A$ and $B$ change:
Can you justify your answer?
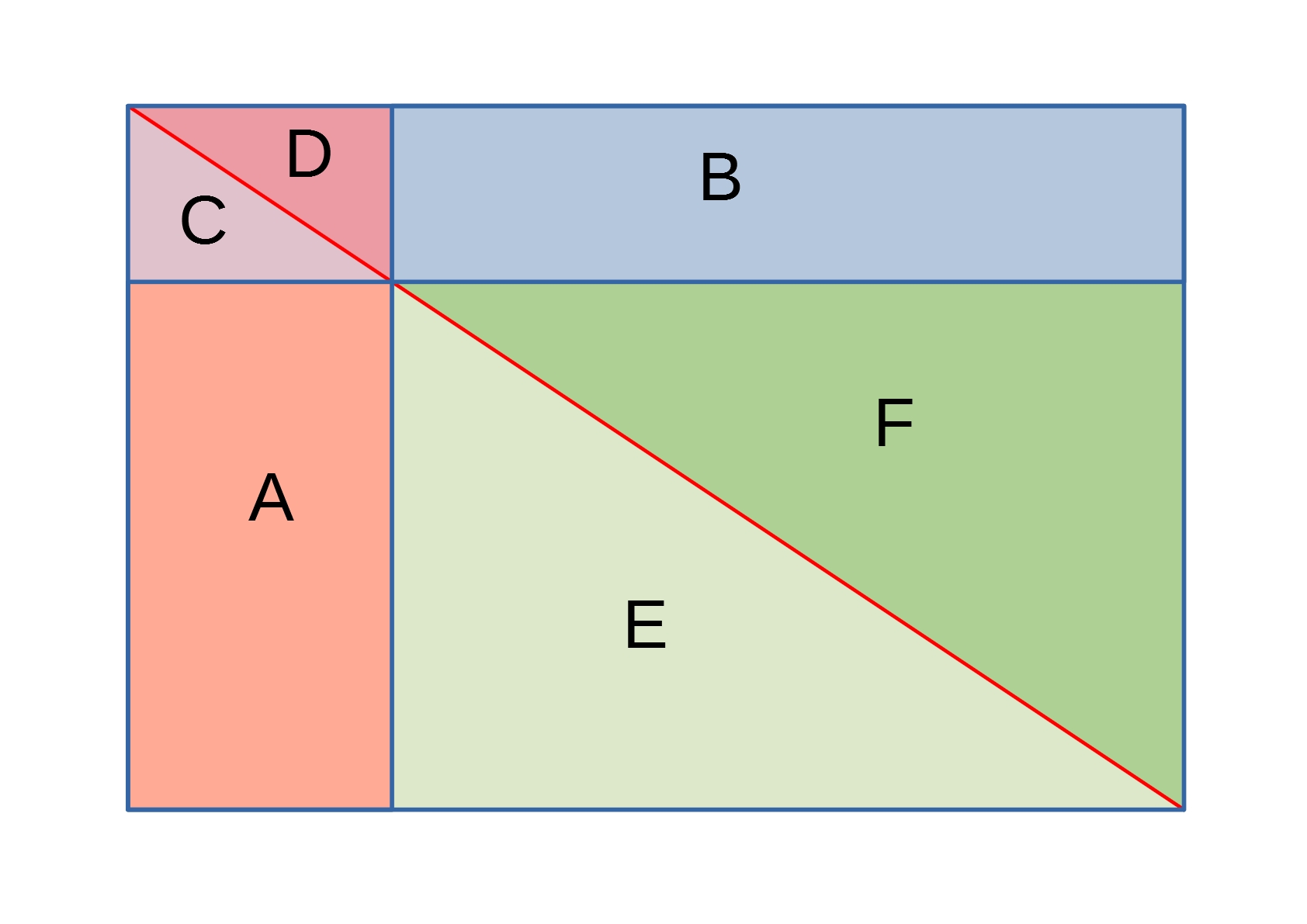
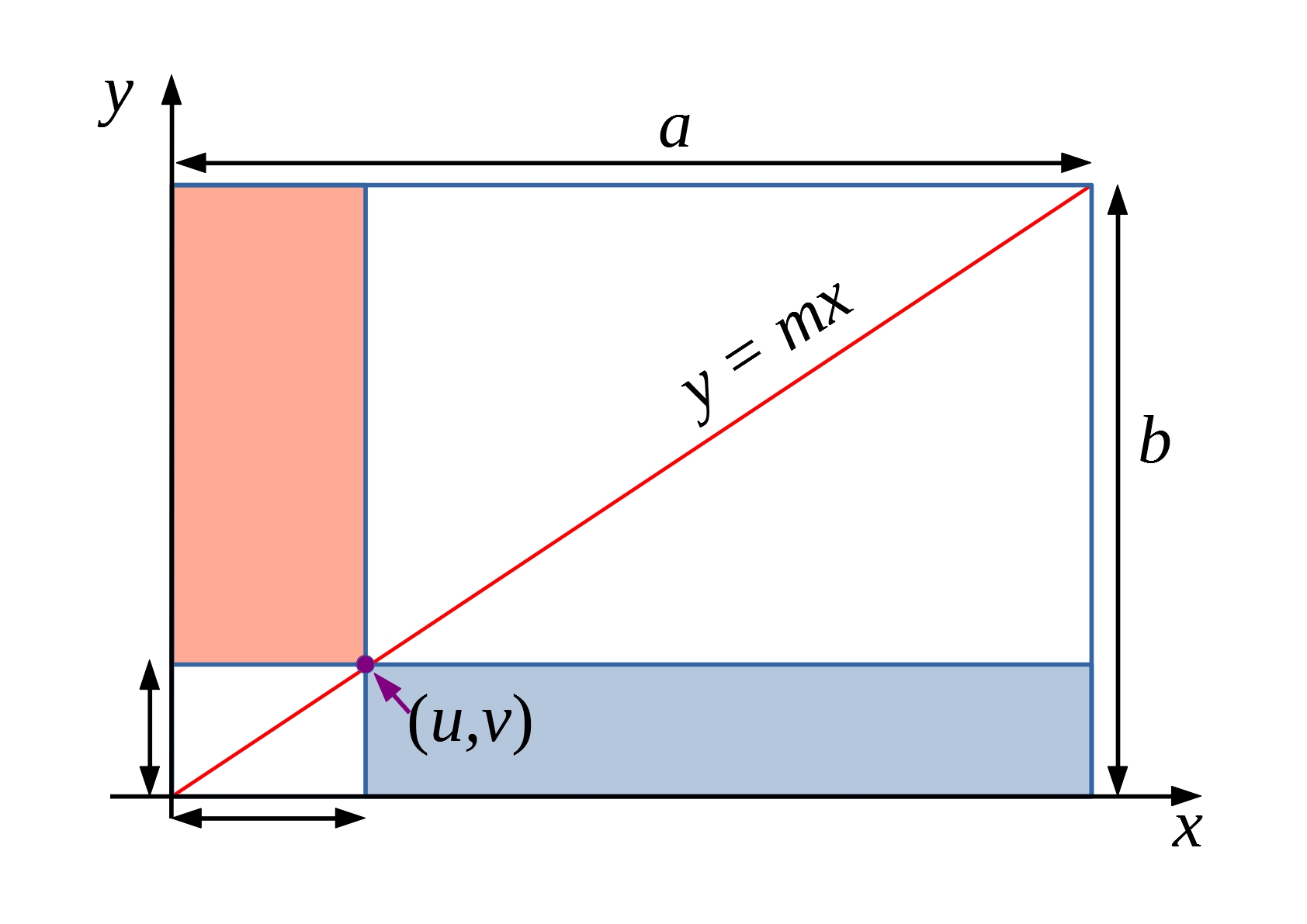
Can you use the diagrams below to justify your results in two different ways?
You may also like
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?
