Sliding Rectangles

Hannah from the UK, Oli from Eltham College, Ali from Langley Grammar School, Saanvi from Newcastle under Lyme Prep School and Dylan from Brooke Weston, all in the UK, and Anil solved the problem by finding congruent rectangles and triangles. 

Anil wrote:

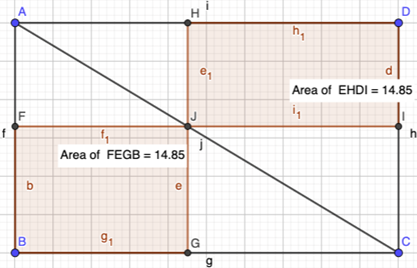
In a rectangle, a diagonal divides a rectangle in two congruent triangles of equal area. Hence:
1. Area triangle ABC = Area Triangle ADC
2. Similarly GJIC is a rectangle, therefore Area triangle JGC = Area triangle JIC
3. Similarly AHJF is a rectangle, therefore Area triangle AFC = Area triangle AHJ

Now subtracting the sum of 2 and 3 from 1, we get Area rectangle FBGJ = Area rectangle HJID

Hannah's proof goes into more depth and includes rigourous proofs of Anil's three statements. Note that Hannah used different letters to label the shapes (click on each image to see a larger version):

Cosima from the UK used ratio:

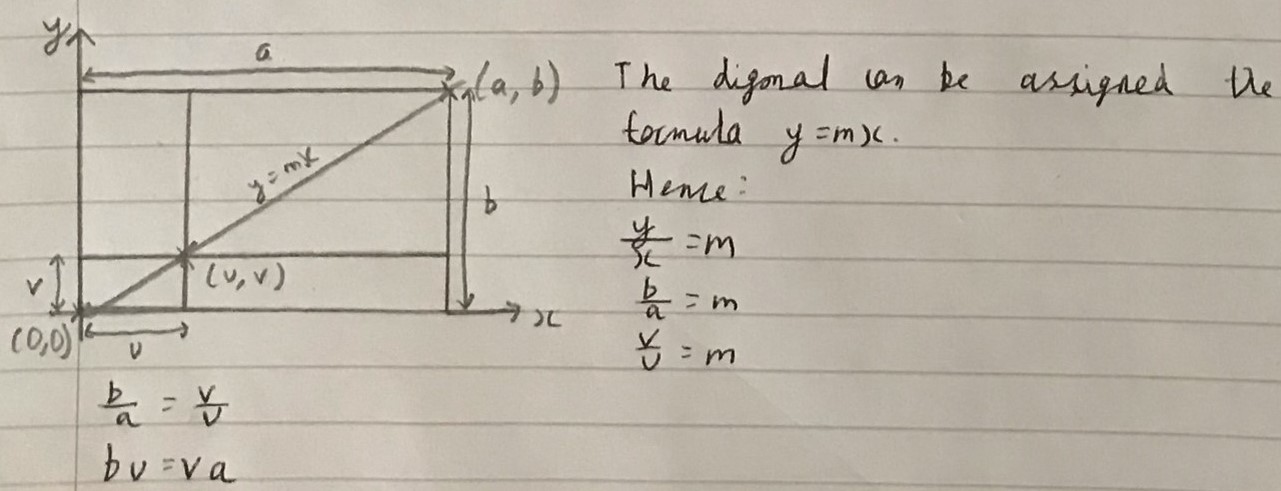
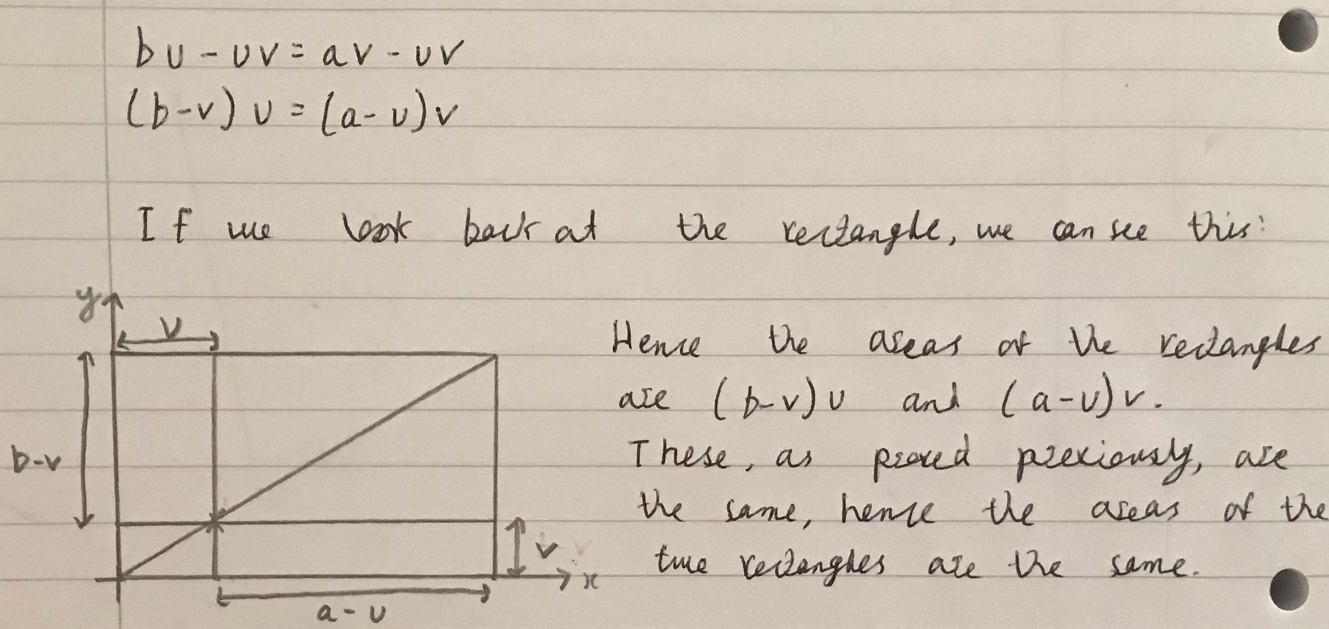
Ali and Oli used coordinates to express the same ideas (click on the images to see a larger version). Notice that they turned the picture upside down to keep the algebra simple:

Oli's method is exactly the same, but Oli used the ideas in a different order. Click to see Oli's work.

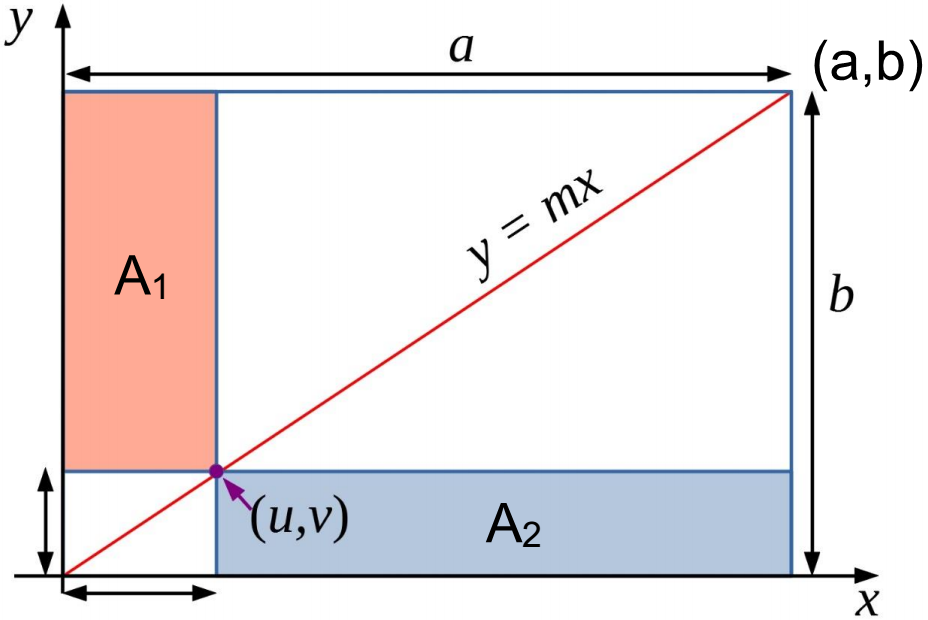
Consider expressions for $\text A_1$ and $\text A_2,$ $$\text A_1 = u(b-v) = bu-uv \\ \text A_2 = v(a-u)=av-uv$$
Considering the line $y = mx$ at $(a,b),$ $$b = m\times a \\ m = \tfrac ba $$
Therefore, at $(u,v),$ which is on $y = mx,$ $$v=\tfrac ba u \\ av=bu$$
Substituting into expressions for $\text A_2,$ $$\text A_2 = bu-uv$$
Therefore, $$\text A_1=\text A_2$$

Dylan kept the rectangle the original way up, and worked through tougher algebra:

We can begin by drawing a graph containing the rectangle with its bottom left corner placed on the origin, and naming the width and height of the rectangle $m$ and $n.$ Drawing on the diagonal of the rectangle, we obtain the following diagram:

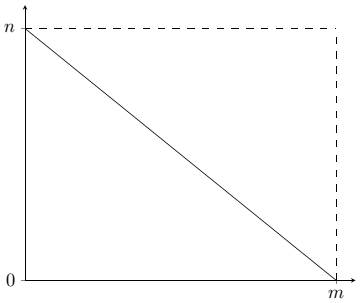
We can see that the diagonal contains the points $(m,0)$ and $(0,n).$ Therefore, we can find the gradient of this line, which is $-\frac nm.$ Using $y=mx+c$ with $'m'=-\frac nm$ and $'c'=n,$ we obtain the equation $$y = n - \tfrac nm x\hspace{40mm}(1)$$ We can label a general point $\text P$ on this line, with coordinates $(x,y),$ and draw out the rectangles $\text A$ and $\text B$ from this point.

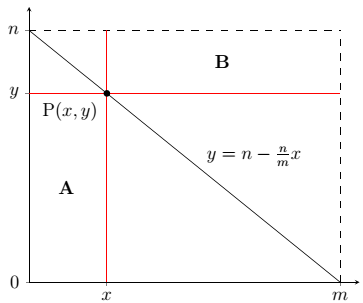
Now, we can see that the area of rectangle $\text A$ is given by $A = xy$ and the area of rectangle $\text B$ is given by $B = (m-x)(n-y)$ from the diagram. As we know that $y = n - \frac nm x$ for every point on the diagonal, we can substitute equation $(1)$ in the expressions for the areas of the rectangles. By doing this, we get $A = x\left(n-\frac nm x\right)$ and $$\begin{split}B&=(m-x)\left(n-\left(n-\tfrac nm x\right)\right)\\&=\tfrac nm x \left(m-x\right)\\&=x\left(n-\tfrac nm x\right)=A\end{split}$$
Therefore the answer to the problem is that the two areas are equal, no matter which point P on the diagonal you choose, and no matter what the dimensions of the big rectangle are.
 

Quinn from the UK used algebra and ratio in a slightly different way:

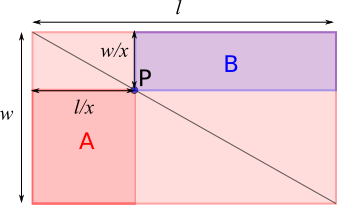To work out the areas of the rectangles, we need a formula for the area of each rectangle. Here are the steps I took to find that.

1. I labelled the sides of the rectangle $l$ and $w.$
2. Because of the nature of diagonals, P is $\frac l x$ units from $w$ and $\frac w x$ units from $l.$ $x$ is an arbitrary amount but it remains the same.
3. The short side of A can therefore be labelled $\frac l x,$ and the short side of B labelled $\frac w x.$
4. The long side of A can be labelled $w - \frac w x,$ and the long side of B labelled $l - \frac l x.$
5. The area of A is therefore $\frac l x \left(w - \frac w x\right)$ and the area of B is $\frac w x \left(l -\frac l x\right).$
6. Simplifying this, we get $\frac{lw}x - \frac{lw}{x^2}$ and $\frac{lw}x - \frac{lw}{x^2}.$
7. This shows that both rectangles are equal sized, so neither is bigger than the other.