Triangle in a Trapezium

Age 11 to 16

Challenge Level Yellow star

You may find it useful to print off some dotty paper or use the dotty grids environment to explore the first part of this problem.

Triangle in a Trapezium printable sheet - problem introduction
Triangle in a Trapezium printable sheet - starting points

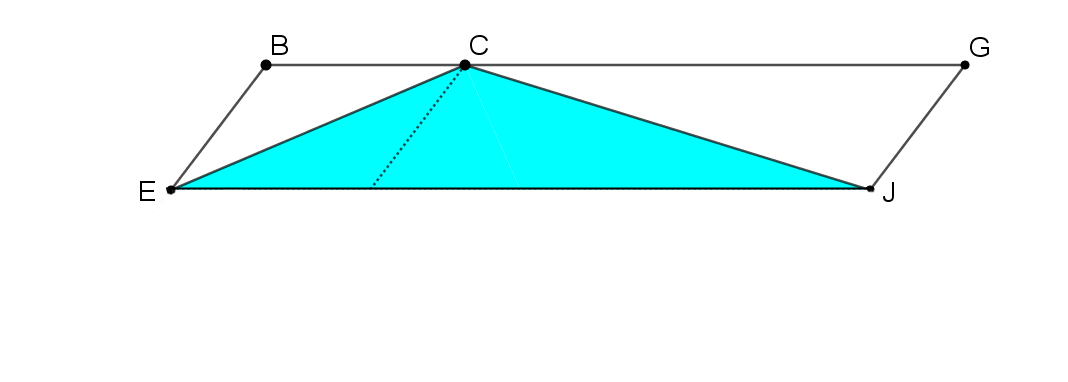
In the two trapeziums below, we have drawn triangles by joining the vertices of one of the non-parallel sides to the midpoint of the opposite side.

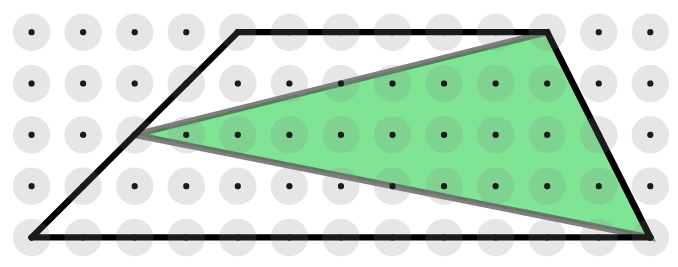
Trapezium, parallel sides length 6 and 12, height 4 units. The midpoint of the left side is joined to the vertices on the right side to form a triangle, shaded green.

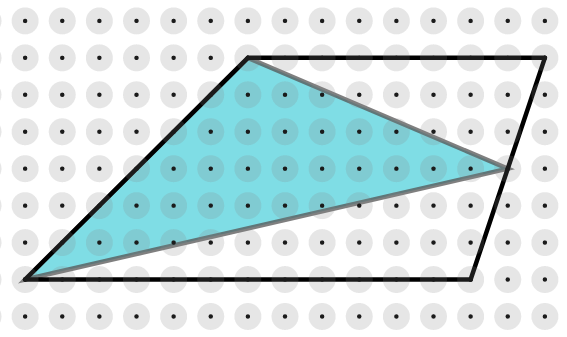
Is there a relationship between the area of each trapezium and the area of the shaded triangle contained within it?

Draw some more trapeziums and construct triangles inside them in the same way. Does the same relationship hold?

Can you find a way to prove that your relationship will always hold for any trapezium?

Once you have had a go at proving it, click below to see some possible starting points.

Can you take each starting point and develop it into a full proof?

Starting Point 1

In this diagram, an extra line has been drawn joining E, the midpoint of AB, to F, the midpoint of CD.

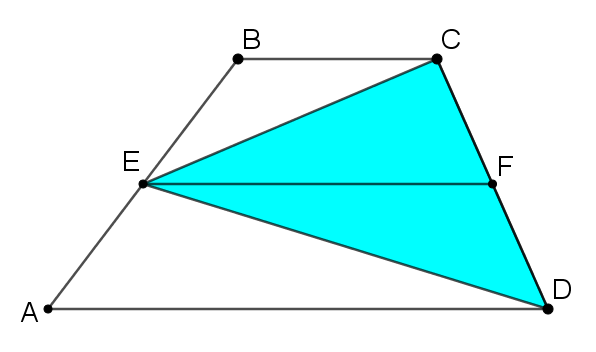
Trapezium ABCD, AB has midpoint E and CD has midpoint F. Triangle CED is shaded blue. Line EF is marked.

Trapezium ABCD, AB has midpoint E and CD has midpoint F. Triangle CED is shaded blue. Line EF is marked.

How could you use this diagram to show that the area of the triangle is half the area of the trapezium?

Starting Point 2

Take a look at this sequence of three images. What happens at each stage?

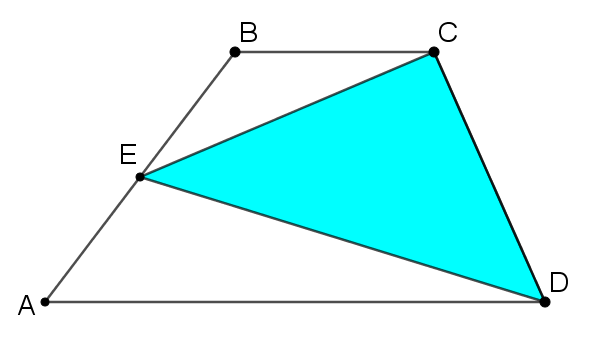
Trapezium ABCD, E is the midpoint of AB, Triangle CED is shaded blue.

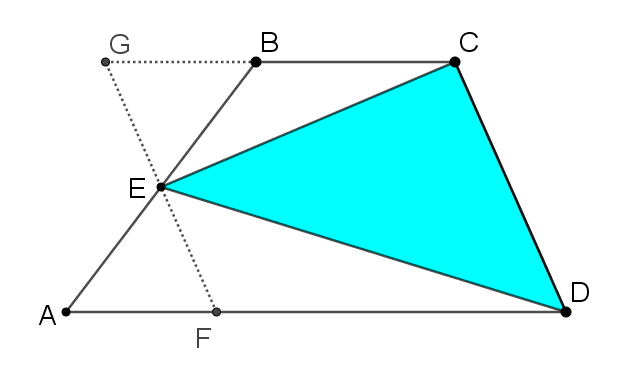
Trapezium ABCD, E is the midpoint of AB. The line through E parallel to CD has been added. It intersects AD at F, and the continuation of BC at G.

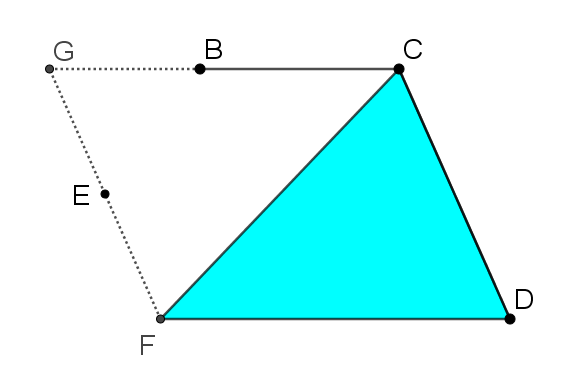
Lines from the previous picture have been erased to leave parallelogram FGCD. Triangle FCD is shaded in the same blue as the original triangle in the first image.

How could you use this sequence of three images to create a proof that the area of the triangle is half the area of the trapezium?

Starting Point 3

Take a look at the image below. Can you see how the trapezium ABCD has been transformed to create this image?

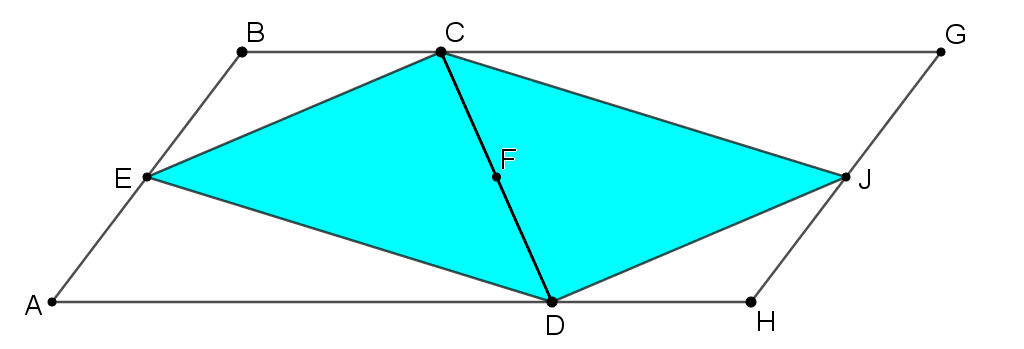
Trapezium ABCD, E and F are midpoints of AB and CD. Triangle CED is shaded blue. The whole shape has been rotated 180 degrees around point F.

Trapezium ABCD, E and F are midpoints of AB and CD. Triangle CED is shaded blue. The whole shape has been rotated 180 degrees around point F.

How could you use this image to prove that Triangle CED has half the area of Trapezium ABCD? Click below to show two more images that might help.

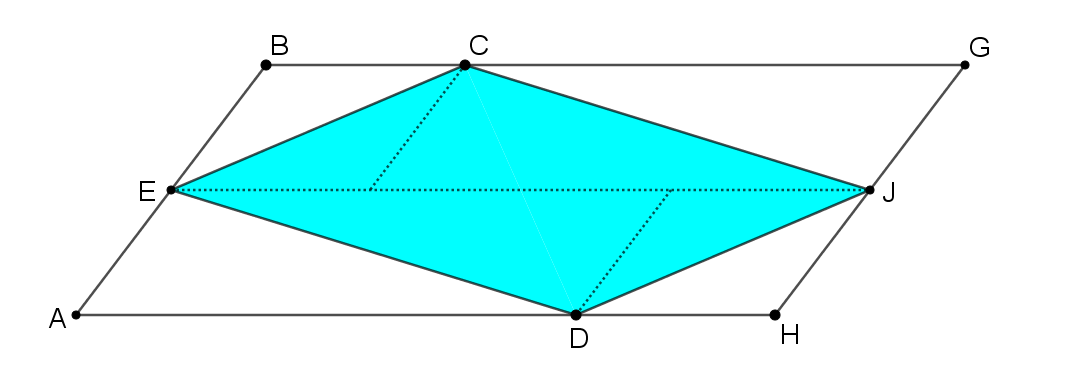
The previous picture now has a line through E and F which continues to the point J (the rotated point E), and lines parallel to AB passing through C and H (the rotated point B)

AEFD has been rotated 180 degrees around F to create a parallelogram EBGJ. Triangle ECJ is shaded blue.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Triangle in a Trapezium

You may also like

Fitting In

Look Before You Leap

Triangle Midpoints