Triangle in a Trapezium

Thank you to everyone who sent in their solutions to this problem. We received either full or partial solutions from Sammy at Lancing College; Tobias and Ana (no schools given); Sanika from PSBBMS in India; and Quang from the British Vietnamese School in Vietnam. As you discovered, there were several ways to prove this result and we suggested three possibles approaches. 

Method One

For this method, we suggested drawing an extra line joining E and F, the midpoints of AB and CD respectively.

Several of you suggested that it would be helpful to explore another relationship before going any further. For example, Sanika noted the usefulness of exploring "a relationship between the lengths of BC, EF and AD and also figure the heights of the two smaller trapeziums."

Well spotted, Sanika and everyone else who realised that this would be useful. This relationship, which several of you uncovered in different ways, is known as the mid-segment theorem for trapezia and it can be very helpful for Method 1. It states that if a line connecting the midpoints of the two legs of a trapezium is parallel to the bases, then its length is equal to half the sum of the lengths of the bases.

Sammy, from Lancing College, made good use of this theorem in this solution: 

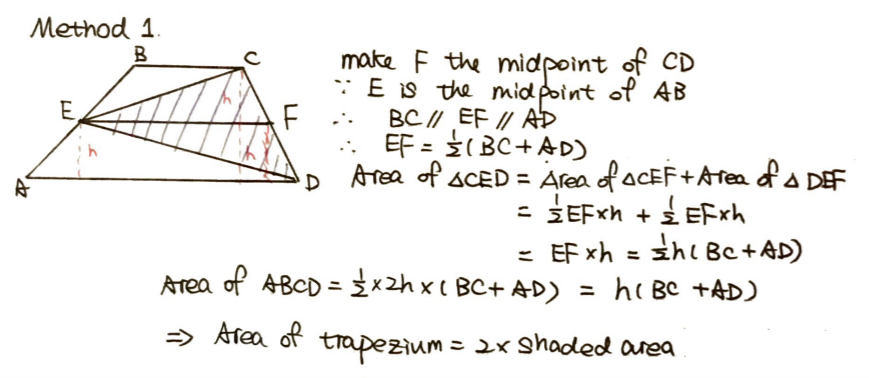
Method Two

Well done to everyone who followed the sequence of images to explore Method Two. 

Here's how Sanika approached the problem using Method 2:

To prove that the resultant figure GCDF is a parallelogram, we would have to prove that the triangles EAF and EBG are congruent.

AE = BE (as E is the midpoint of the line segment AB)

Angle GEB = Angle FEA (Vertically opposite angles)

GB and AF would be parallel as they are extensions of parallel lines. Therefore, we can say that angle GBE = angle FAE as they are alternate-interior angles.

Therefore Triangle EAF is congruent to triangle EBG.

This implies that the area of the trapezium is the same as the area of the parallelogram.

We can then invert the parallelogram so that the base and height of both the parallelogram and the triangle would be the same measure.

Let base be 'b' and let the height be 'h'.

Therefore the area of the parallelogram = bh

Area of the triangle = bh/2

Since the area of the parallelogram is the same as the area of the trapezium we can say that the triangle is half the area of the trapezium.

Method 3

Here's Sanika's sketch:

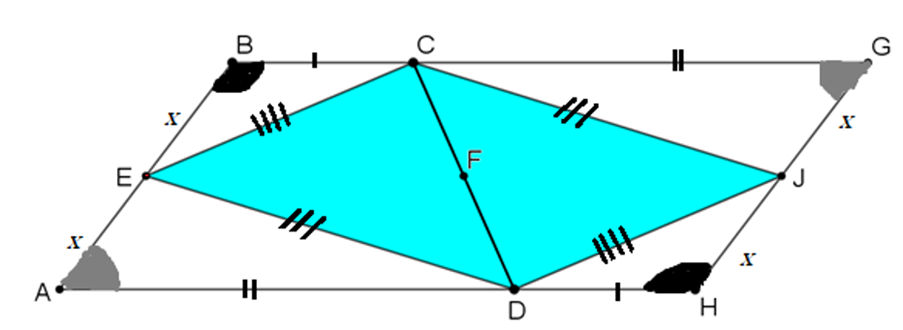
Have you noticed how Sanika has annotated our original diagram to help her solve the problem? A good sketch is always worth the time spent on it. 

From the diagram, we can tell that the line segment BG will be equal to line segment AH. They will also be parallel as opposite sides of a Trapezium are parallel. Since we have one pair of opposite sides which are parallel and equal, we can deduce that the quadrilateral ABGH is a parallelogram.

Once she was convinced that the shape was a parallelogram, Sanika followed the hints provided for Method 3:

As opposite angles of a parallelogram are equal, the following will hold true:

Angle B = Angle H

Angle A = Angle G

Using the SAS [side-angle-side] congruence criteria, we can say the following:

Triangle EAD is congruent to triangle JGC (Thus, line segment ED = JC)

Triangle CBE is congruent to triangle DHJ (So line segment CE = DJ).

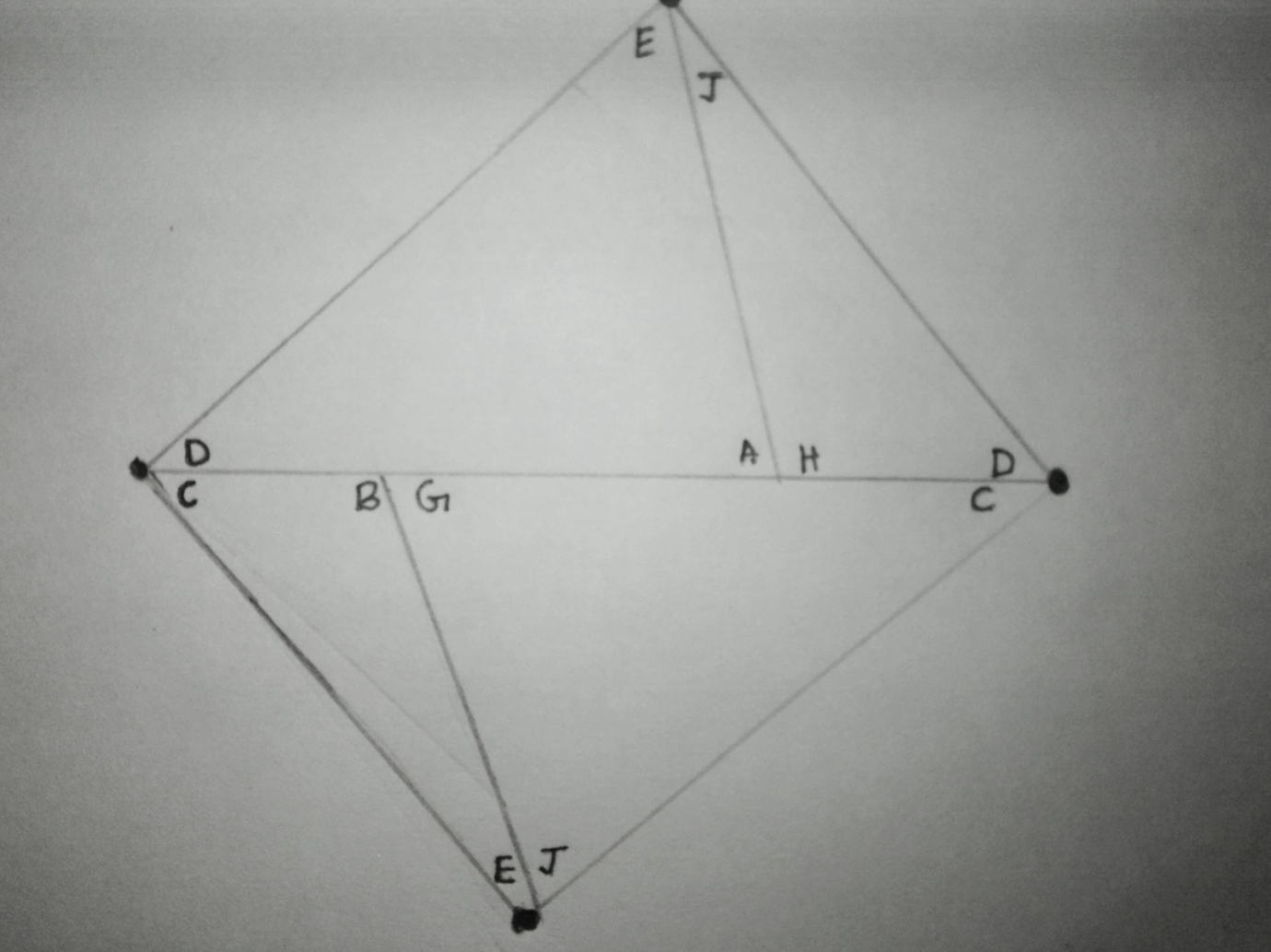
We can then rearrange triangles CBE, CGJ, AED and DHJ, as shown in the image above, to form the quadrilateral DECJ (or CJDE).

Since AE and HJ are of the same length 'x', we can join them together.

Similarly as BE and GJ also share a length of 'x', we can join them together.

As proved earlier, triangle EAD is congruent to triangle JGC and triangle CBE is congruent to triangle DHJ so the bases will be the same, in which case we can join them to form the quadrilateral DECJ.  This is identical to the two triangles contained in the trapezium, put together.

Therefore, we can say that the area of the quadrilateral DECJ is half the area of the parallelogram BGHA.

As the parallelogram is just 2 copies of the trapezium, we can say that the area of CED is half the area of the trapezium ABCD.

Well done to Sanika and everyone else who explored this problem. We hope you enjoyed investigating different approaches towards finding a solution.