The Square Under the Hypotenuse
The Square Under the Hypotenuse printable worksheet - initial problem
The Square Under the Hypotenuse printable worksheet -different methods
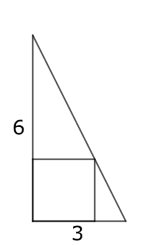
This right-angled triangle has a base of 3 and a height of 6 units.
How might you construct the square, which just touches the hypotenuse?
Can you work out the side length of the square?
Can you think of more than one way to work it out?
What if the side lengths of the triangle were 12 and 4 units long?
What if they were $a$ and $b$ units long?
Once you've had a go at solving this, click below to reveal three different approaches.
Can you take each starting point and turn it into a solution?
Method 1
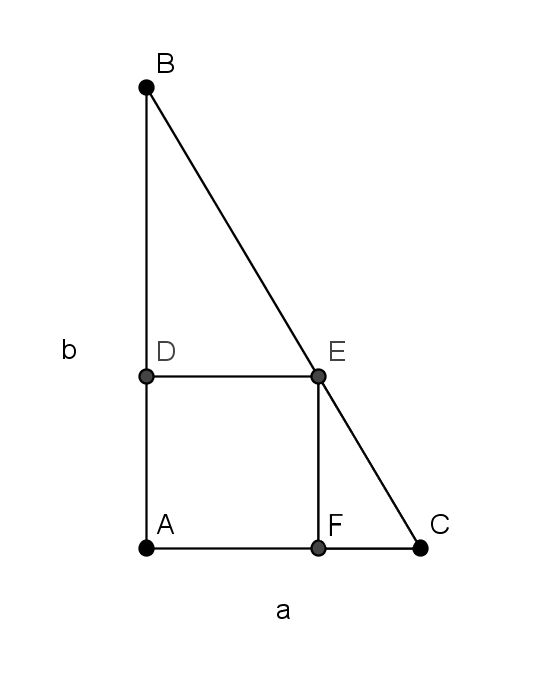
There are some similar triangles in the image below.
How could you use these similar triangles to find the side length of the square?
Method 2
We can draw the triangle on a set of coordinate axes.
What is the equation of the line $BC$?
What do we know about the coordinates of point $E$?
How could you use this to find the side length of the square?
Method 3
Can you see how to create the rectangle on the right from the rectangle on the left?
Find expressions for the areas of the two rectangles.
How could you use these expressions to find the side length of the square?
You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?