The Square Under the Hypotenuse

This was a very popular problem! We received correct full solutions, or partial solutions, from Zhifang and Sevinch from St George's International School Rome; Carlos at King's College, Alicante; Sanika at PSBBMS in India; Shayan and Angus at St Stephen's School, Carramar; Sammy at Lancing College; Max at West Island School in Hong Kong; Xinrong at Howell's School in Wales; Arnik and Viktor at Wilson's School; Chamundeshwari from Wolsey Hall in India; Dibyadeep from Tanglin Trust School in Singapore; and from Wendy, Ananya and Ana (do get in touch to tell us your schools). Well done, everyone.

Exploring different ways to solve a problem can be a fascinating process. Knowing alternative methods can help you to build strong connections between different areas of mathematics as well as ensuring that you have other approaches to explore when you get stuck (which happens to us all!).

This particular problem challenged you to explore three different methods and we received solutions for each of the methods. Clearly some of you preferred one method over another, depending on your past experiences and favourite ways of working. Do read through each of the approaches below and perhaps try them out for yourself.

Method 1

Method 1 suggested exploring an approach using similar triangles. This was a popular approach, and it was pleasing to see how many of you remembered to check that you did indeed have similar triangles rather than simply assuming that they were similar.

Here's Sammy's approach for finding the length of the side of the square using Method 1:

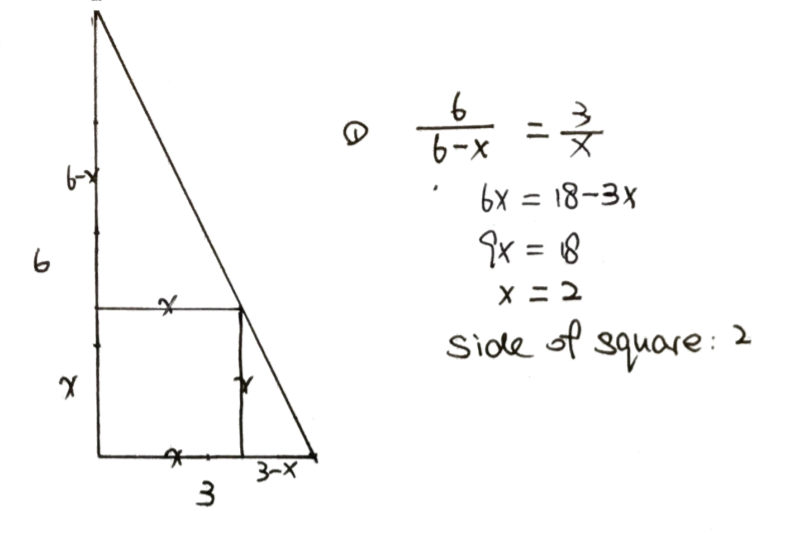
Method 2

The hint for Method 2 suggested adopting an approach using co-ordinates. Here's Ana's solution for Method 2:

In this case, where a = 6 and b = 3,
p = $\frac{18}{9}$ = 2

Thank you, Ana.

Method 3

Method 3 suggested trying to create rectangles. Here's Sanika's approach using that method:

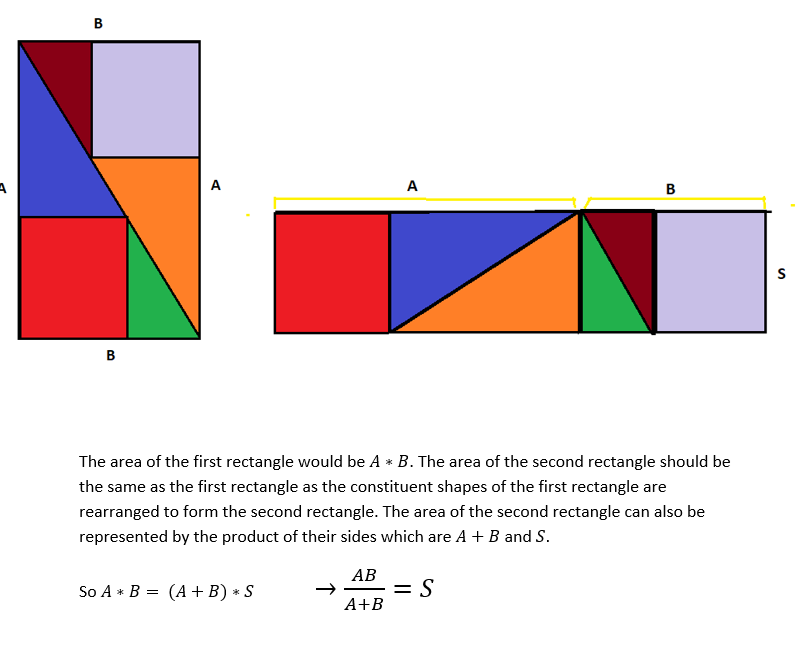
In this case, where A = 6 and B = 3,
$S = \frac{AB}{A+B} = \frac{18}{9}$ = 2
 

Having had a chance to read through these solutions, which use three very different methods, which do you prefer and why?