The Square Under the Hypotenuse

Why do this problem?

Students often think that there is only one correct way to approach a geometrical challenge. This problem poses a geometrical problem and offers three starting points that lead to different methods to solve it. We hope this will encourage students to reflect on what might be their preferred approach and why, and for them to develop a flexible attitude to geometrical problem solving.

Possible approach

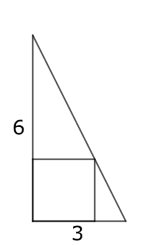
Start by showing this right-angled triangle, and inviting students to discuss how they would construct the square so that it just touches the hypotenuse. This could be a good opportunity to practise some construction techniques.

Next, pose the main problem; we could find the side length of the square by measuring, but this might not be accurate. Is there a way we can calculate the side length of the square using geometrical reasoning?

Give students some time to explore ideas. In the problem, there are starting points for three different methods:

• Using similar triangles
• Drawing the triangle on coordinate axes and finding the point of intersection of the hypotenuse with the line $y=x$
• Rotating the triangle to make a rectangle, then cutting up and reassembling the rectangle and equating areas.

These starting points could be used for the particular case of a triangle with side lengths 6 and 3, the suggested follow-up 12 and 4, and then for the general case with side lengths a and b. (We chose 6 by 3 and 12 by 4 as they give integer answers for the side length of the square.)

Once student have had a go at finding the side length of the square using all three methods, set aside some time to discuss which method they preferred, and why. This reflection will help them to develop a toolkit of geometrical problem-solving techniques that they can apply in future situations.  

Key questions

Method 1:
If the square has side length $x$, what are the side lengths of the smaller triangles?
How do we know the triangles are similar?
Using the fact that the triangles are similar, can we write any equations involving $x$?

Method 2:
If we draw the triangle on a coordinate grid, with the right angle at the origin, what are the coordinates of the vertices of the triangle?
How can we work out the equation of the hypotenuse?
What would the equation of the diagonal of the square be?

Method 3:
What is the length and width of the original rectangle?
What are the dimensions of the rearranged rectangle?
Can you use the fact that the areas are the same to write an equation?
 

Possible support

Some students might find it helpful to draw the 6 by 3 and 12 by 4 triangles on squared paper to see the similar triangles and intersecting lines.

Possible extension

Students could consider which other dimensions of triangle will produce a square with a side length that is an integer.
Squirty explores construction of a square in any triangle, and might be a good follow-up challenge.
Compare Areas requires similar geometrical reasoning.