Geometry in the Primary Curriculum

The Mathematics National Curriculum for primary children in England aims to ensure that all pupils:

• become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
• reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language
• can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

In this article, part of our Jaunts into Geometry Feature, we will look at how these aims of problem solving, reasoning and fluency can be embedded in geometry, using NRICH tasks. In the classroom, this might be achieved in two ways, depending on the focus of a particular lesson or series of lessons, by exploring:

1. Problem solving, reasoning and fluency in a geometrical context
2. The geometrical strands of the National Curriculum in a problem-solving context.

Let's look at each of these in turn.

1. Exploring problem solving, reasoning and fluency in a geometrical context
There are many tasks on the NRICH site, which are set in geometrical contexts, and which are ideal for supporting the National Curriculum (NC) aims. 

The game Seeing Squares is a great context in which to focus on problem solving, for example by explicitly talking about the problem-solving skills learners need in order to work out a winning strategy.  Visualisation and working systematically are likely contenders, and you could follow up this game with the task Square Corners, which might further develop these two problem-solving skills and additionally trial and improvement. 

If you are looking to focus on reasoning in a geometrical context, try Jig Shapes.  It will give learners opportunities to develop their vocabulary and language associated with describing, explaining and convincing so that they get better at communicating their reasoning. 

Stringy Quads invites children to work together in a group to create symmetrical quadrilaterals using a loop of string.  It is particularly good for developing fluency with geometrical ideas.  It might be tempting to think that fluency only applies to number and calculation however, at NRICH, we have a wider view of fluency than that.  In the context of Stringy Quads, learners are becoming more fluent with concepts (such as representations of quadrilaterals and symmetry); and even becoming more fluent in making connections across different areas of mathematics.  In this case, connections might be made which link the number of sides with the number of possible lines of symmetry.  Some children might even conjecture that a shape with n sides can never have n-1 lines of symmetry, even if they cannot quite explain why.


2. Exploring the geometrical strands of the national curriculum in a problem-solving context
If your main objective for a lesson or a series of lessons is to deepen children's knowledge and understanding of a particular aspect of geometry, then you can still do this through problem solving.  By engaging with rich geometrical tasks, learners will not only grapple with geometrical concepts and further their own understanding, but they will also have opportunities to refine their problem-solving skills. Many NRICH tasks help to meet objectives in the geometrical strands of the NC.

The National Centre for Excellence in the Teaching of Mathematics (NCETM) has published 'progression maps' on their website which illustrate progression in key areas (you will need to be registerd with NCETM to view them).  They have split up the elements of the geometry NC into two categories:

• properties of shapes, which includes identifying shapes and their properties, drawing and constructing, comparing and classifying, and angles
• position and direction, which includes transformations, coordinates and pattern. 

We have found these progression maps very helpful and we use their terminology in this article.

Before taking a look at some further NRICH tasks which might support different aspects of geometry, let's briefly consider the tasks we looked at above from a curriculum 'content' perspective. All three of them (Stringy Quads, Seeing Squares and Jig Shapes) focus on properties of shape and Stringy Quads also involves comparing and classifying, and of course symmetry.  A discussion about properties of shapes often proves to be a useful opportunity to tackle misconceptions, such as the meaning of words like 'regular', which have a particular mathematical definition apart from their common English usage.  A rectangle is not a regular shape in the mathematical sense!

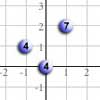What about NRICH tasks to support other areas of the geometry curriculum?  If you are focusing on coordinates, there are several intriguing activities to draw to your attention.  In Cops and Robbers, learners are asked to find the robber who is hiding at the crossroads of a city, represented by a square grid.  It challenges learners, not just to use their knowledge of coordinates, but to think strategically and reason logically.  Eight Hidden Squares will also support learners' knowledge of the coordinate system and, in addition, entails using properties of shapes.  The challenge is to find the eight squares on the grid, knowing only their vertices, so learners are likely to use some trial and improvement, combined with a systematic approach.  (Ten Hidden Squares is a natural follow-up task.)

If you are searching for tasks that will support children's understanding of angles at the same time as helping them develop their problem-solving skills, you could start with Turning Man.  This makes a bridge between children physically turning to experience angles themselves and applying turns to a picture.  Olympic Turns is a very open task, inspired by the Olympic Games, which invites learners to look for angles in different sports, estimate their sizes and even find ways of measuring them (from photos).  National Flags provides a context for exploring a range of aspects of the geometry curriculum and could, for example, make a nice task for the beginning of a series of lessons so you can assess what children already know.  As well as including opportunities to discuss angles, learners will be identifying shapes and their properties, and exploring symmetry.

Repeating Patterns, as the name suggests, encourages children to recognise, make and describe repeating patterns (in this case using triangles) and then challenges them to create repeating patterns of their own.  Creating their own patterns may provoke discussions about the properties of the particular triangles given and this may prompt them to ask their own "what if ...?" questions.

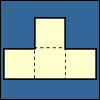If you are looking for rich tasks to help children get to grips with 3D shapes, Cut Nets is a great choice.  The nets of nine solid shapes have each been cut into two pieces and learners are asked to pair them up.  This task moves beyond identifying 3D shapes from their nets as learners' visualisation skills will be put to the test trying to match two pieces of a net together.


We have created a downloadable grid which links NRICH tasks to the NC programmes of study for geometry.  This makes it clear that, as alluded to above, a single NRICH task can help address a number of different concepts but also offer opportunities for learners to be engaged in meaningful problem solving.

Remember that every NRICH task has accompanying 'Teachers' Resources', which can be accessed by following the link in the left-hand menu once you are viewing a task.  There you will always find a 'Why do this problem?' section, which not only outlines the currriculum content of the task in terms of number/measurement/geometry/stastics but also gives you some guidance on the possible problem-solving skills which could be developed through that task.


Geoboards: a key resource
Having outlined how the NC aims can be embedded in geometry using examples from NRICH, we cannot conclude this article without mentioning geoboards (or pegboards, as they are sometimes known).  Geoboards are an invaluable resource for exploring geometrical ideas, particularly properties of shapes, angles and area, and we have put together a Geoboards Feature, which includes:

• Take a ”¦ Geoboard, an article, written for primary teachers
• A virtual geoboard
• A range of tasks including Inside Triangles and Nine-pin Triangles, which are both excellent for encouraging children to work systematically to find all possibilities while considering properties of shapes.

In conclusion
You may wish to consider the activities you use currently to explore geometrical ideas.  How are they already promoting problem solving, reasoning and fluency?  Might they benefit from being adapted?  What is the 'coverage' like across the geometrical strands?

We hope you will be inspired to embed problem solving, reasoning and fluency into geometry in your classroom.


Further reading
Take a look at our Problem Solving Feature, which includes the article Using NRICH Tasks to Develop Key Problem-solving Skills.
For further support on developing learners' mathematical reasoning, see our Reasoning Feature.
You may also be interested in our Number Fluency Feature.


References
DfE (2013) Mathematics programmes of study: Key stages 1 and 2 National Curriculum in England https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/335158/PRIMARY_national_curriculum_-_Mathematics_220714.pdf


Here is a PDF version of this article.