Next-door Numbers

Florence chooses a number and then counts on one more:

 

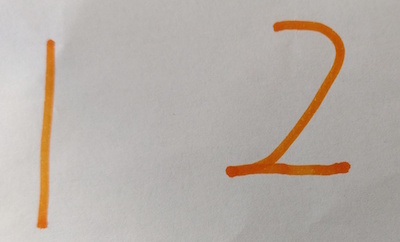
She adds them together and this is what she records:

 


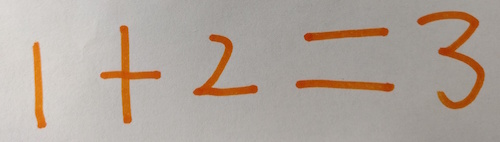
Ethan chooses two different 'next-door' numbers:

 

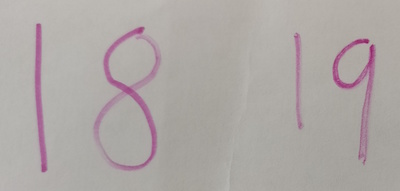
And then he adds them together and records the addition:

 


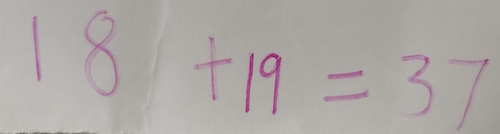
Here are the 'next-door' (consecutive) numbers that Alma chooses:

 

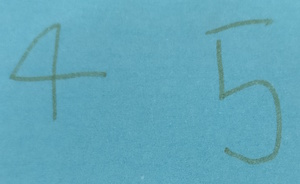
She adds her numbers together:

 



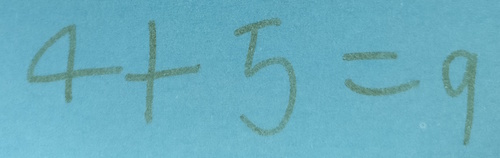
Try this for yourself.  Choose two consecutive numbers and add them together.

What is the same about all the answers?
Does this surprise you?
Will this always happen when you add two consecutive numbers together?

Try drawing a picture or making a model to explain your thinking.
Can you convince someome else using your picture/model?

You may be interested in the other problems in our Surprise! Feature.