Next-door Numbers

Well done to everybody who worked out that the answer will always be odd!

Liam from England said:

When you add 2 numbers next to each other their answer will always be an odd number because 15 is an odd number and 16 is an even number they will always add up to become an odd number.

Ariana from Halstead Preparatory School in the UK agreed with Liam:

There are odd numbers when you add next door neighbour numbers because odd plus even equals odd.

Well done to both of you - an odd number plus an even number does equal an odd number! I wonder why next-door numbers always have one odd number and one even number? And I wonder why adding an odd number and an even number makes an odd number?

The next few solutions are also from children at Halstead Preparatory School.

Juliet drew a picture using Numicon shapes to represent the two numbers she was adding:

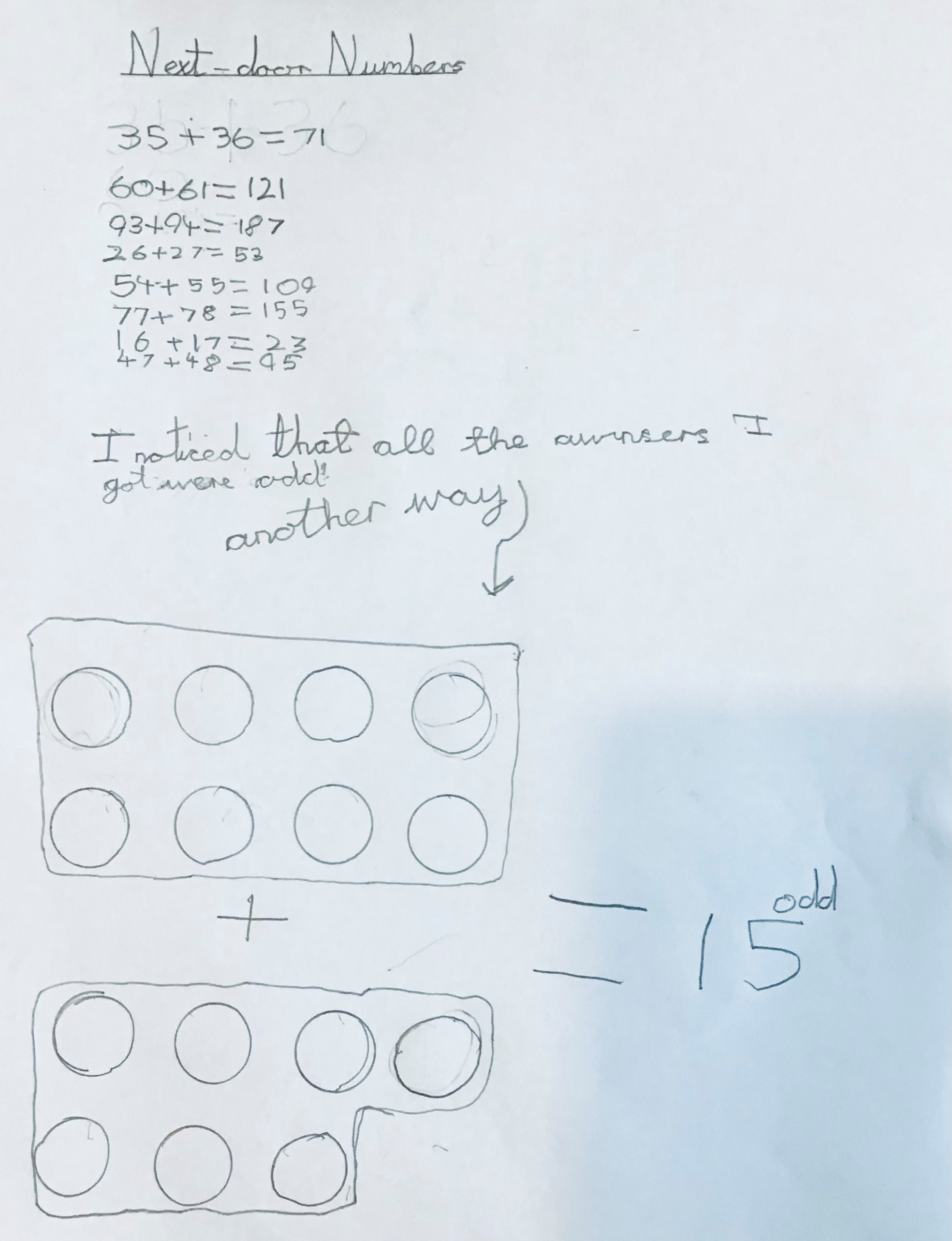
Good idea, Juliet! Can you try representing some other pairs of next-door numbers with Numicon shapes? What do you notice?

Mia drew similar shapes to represent adding 3 and 4:

Well done, Mia! I wonder if we can tell from that picture that 3 is an odd number and 4 is an even number?

Lika used these pictures to represent adding two next-door numbers, where one number has been drawn as red squares and the other number has been drawn as green squares:

This is a good way of representing those numbers, Lika! What do you notice about each picture? Why does this show that the sum of two next-door numbers will be odd?

D from Crossflatts in the UK sent in this explanation:

I noticed that with any next-door numbers, that one number will always be odd and the other will be even. 

If I add two numbers that are the same size together, then the answer is always even. So if I add one number that is odd and another that is even, then I always get an odd number.

Well done, D! I wonder why adding a number to itself always makes an even number?

Viren KS sent in an explanation for why the sum will always be odd using algebra to represent the two next-door numbers. If you have met algebra before, then you might like to take a look. Or you may be curious to look anyway! Click 'show' below to see Viren's explanation.

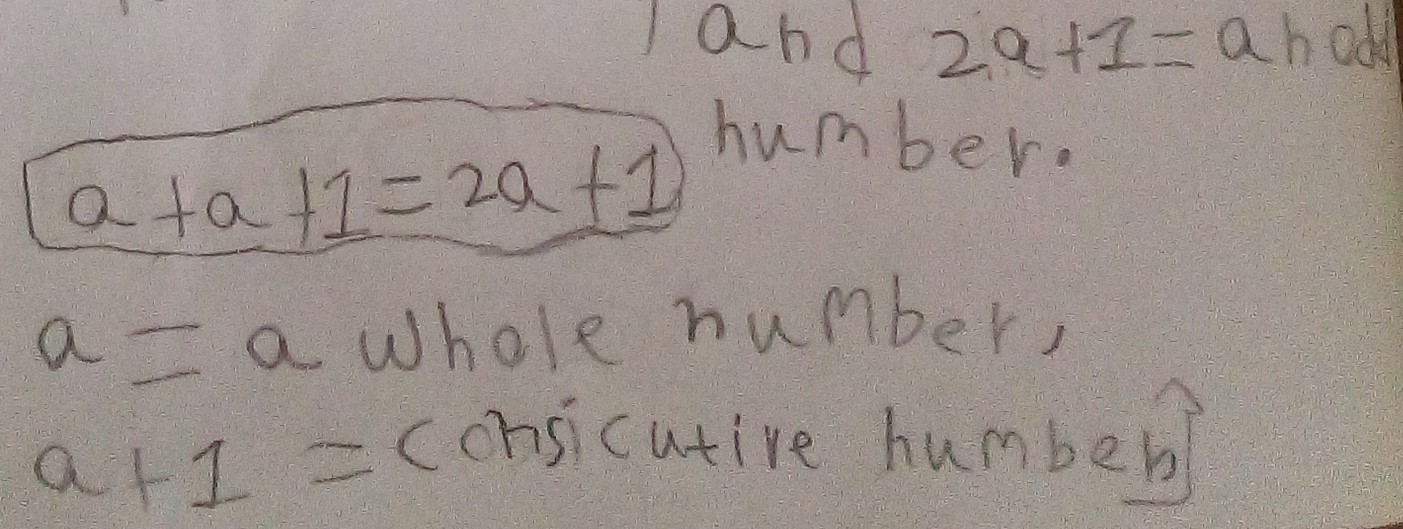
Well done, Viren! Viren has represented a number with the letter 'a', and then the next number will be one more, or 'a + 1'. When we add these together we get a + a + 1, which we can write as 2a + 1. This is an odd number because 2a is in the two-times table, so it is an even number, which means when we add one more we will get an odd number.

Thank you to everybody else who sent in their ideas - we also had excellent solutions sent in by Elena and Eva at Halstead Preparatory School.