Next-door Numbers

Next-door Numbers

Florence chooses a number and then counts on one more: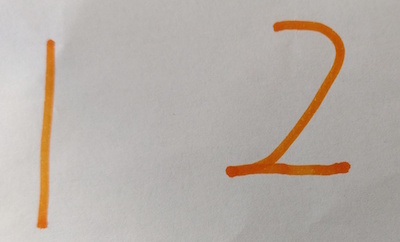

 

She adds them together and this is what she records:

 


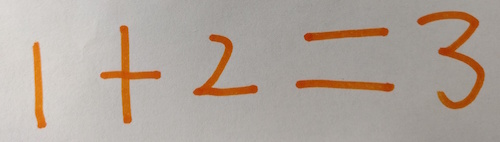
Ethan chooses two different 'next-door' numbers:

 

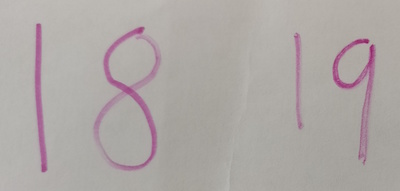
And then he adds them together and records the addition:

 


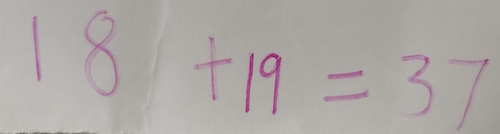
Here are the 'next-door' (consecutive) numbers that Alma chooses:

 

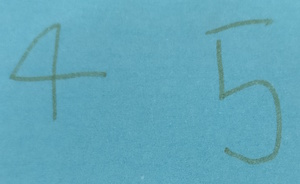
She adds her numbers together:

 



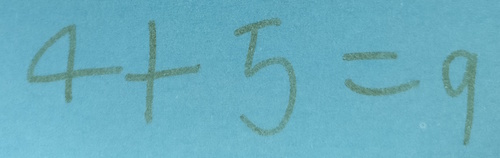
Try this for yourself.  Choose two consecutive numbers and add them together.

What is the same about all the answers?
Does this surprise you?
Will this always happen when you add two consecutive numbers together?

Try drawing a picture or making a model to explain your thinking.
Can you convince someome else using your picture/model?

Why do this problem?

This problem is aimed at young children who are becoming familiar with the concept of odd and even numbers. The outcome (that any two consecutive numbers add to make an odd number) may seem obvious to us, but it is likely to come as a surprise to learners.  The fact that this always happens is unexpected and hooks them in, providing a motivating context in which children can deepen their understanding of our number system and create proofs.
 

Possible approach

Ask everyone to think of two 'next-door' (consecutive) numbers and to add them together.  You could suggest that everyone checks their answers with a partner then invite learners to call them out and write them on the board. What is the same about all these numbers?  If they do not mention that all the numbers are odd, you could mark the answers on a number line, which might help.  

Listen and watch out for children who seem surprised by the fact the answer is always odd. Can they explain why they are surprised? 

Challenge the class to work in pairs to investigate whether this always happens when you add two consecutive numbers together.  If any pair thinks they have found an even total, you could ask them to check with another pair.

Try not to steer them in the direction of particular equipment when you invite them to draw a picture or make a model to explain their thinking. However, if some are really stuck, you could give them a range of classroom resources (e.g. squared paper, Numicon, Multilink...) so they still need to choose which they might use. 
 

Key questions

What is the same about all these numbers?
Will you always get an odd number when you add two consecutive numbers together?
How do you know?
You could choose some equipment to help you make a model or draw a picture.

Possible support

Offering a limited range of equipment, as suggested above, will help some children.

Possible extension

The problem Two Numbers Under the Microscope, which focuses on adding two odd numbers together, would make a good follow-up task at a later stage.