Cyclic Quadrilaterals Proof

 

Why do this problem?

Working on this problem leads students to an accessible proof that opposite angles in a cyclic quadrilateral sum to $180^\circ$. 

Possible approach

This problem follows on from Cyclic Quadrilaterals

“Well we haven't found any examples where the opposite angles don't add up to 180 degrees, but that doesn't mean it will always work - I wonder if we can prove it?”

“Take a look at this diagram and try to come up with a convincing argument that the opposite angles in a cyclic quadrilateral will always add up to 180 degrees.”

 

 

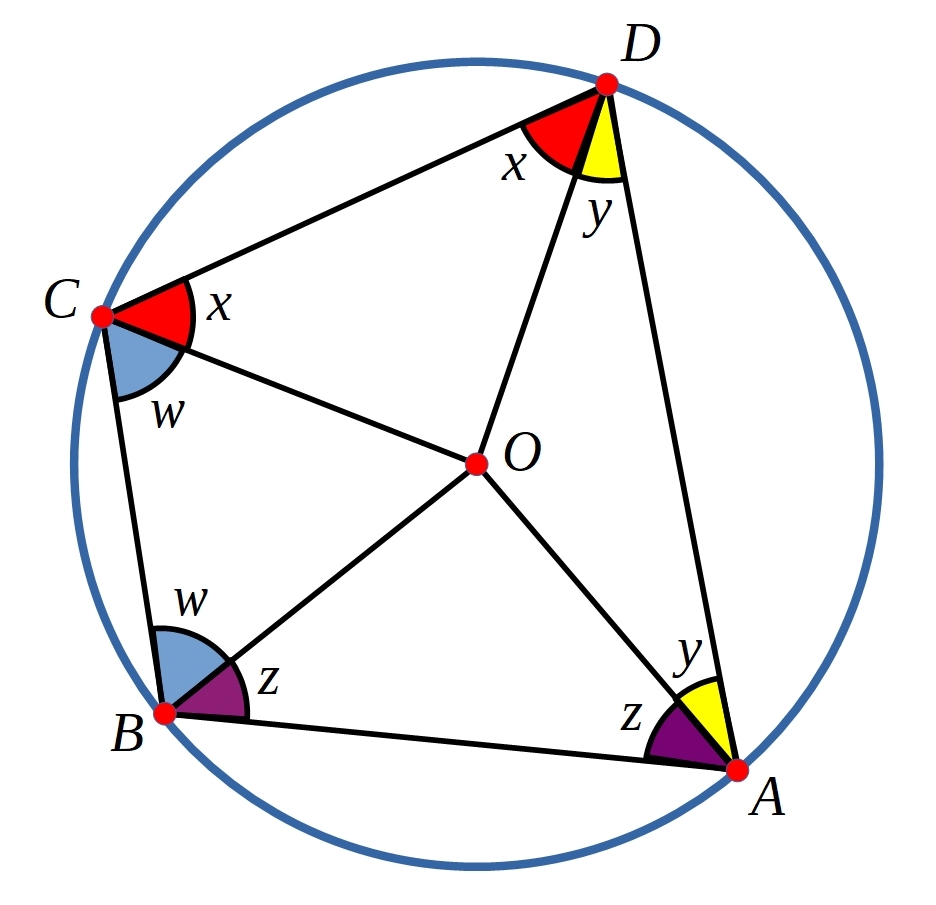
Give students some time to think about a proof. Circulate and look out for students who notice that:

two yellows + two purples + two blues + two reds = 360 degrees
so, one yellow + one purple + one blue + one red = 180 degrees

or

$2w + 2x + 2y + 2z = 360^\circ$
so, $w + x + y + z = 180^\circ$

Opposite angles contain one yellow, one purple, one blue and one red (or one $w$, one $x$, one $y$ and one $z$), so opposite angles add up to 180 degrees.

Bring the class together to share their thoughts.

 

Possible extension

Challenge students to consider whether the opposite angles of cyclic quadrilaterals add to $180^\circ$, when the centre of the circle is outside the cyclic quadrilateral.

Other circle theorems, and an alternative proof to the one suggested in this problem, can be explored in Circumference Angles

The Geogebra app below might be helpful when exploring opposite angles.