Cyclic Quadrilaterals Proof

Sunhari from British School Muscat in Oman and Rohan form Wilson's School in the UK used the same method to prove that opposite angles in a cyclic quadrilateral add up to 180$^\circ$ (assuming the centre of the circle is inside the quadrilateral). This is Sunhari's work (click on the image to see a larger version):

Nayanika from The Tiffin Girls' School Theo from Pate's School in the UK used a different method. This is Theo's proof:

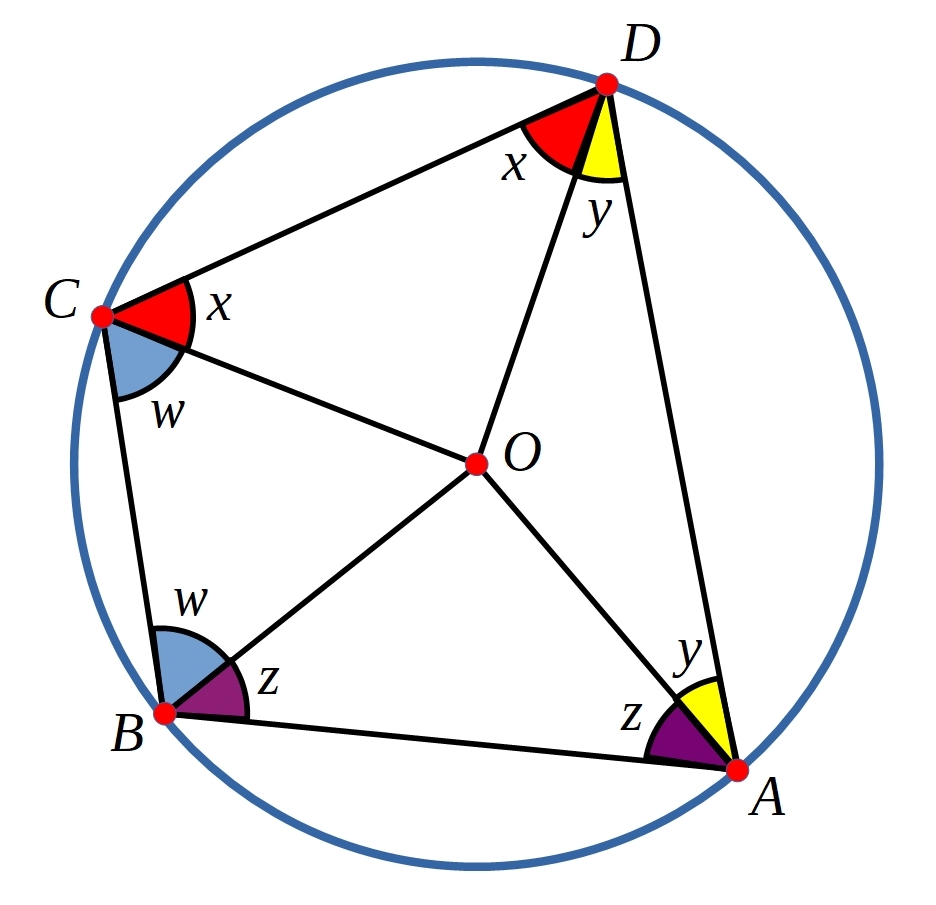
$A+B+C+D$ must equal $360$ as the angles form a quadrilateral. You can also write this as:

$2w+2x+2y+2z = 360$

$2(w+x+y+z) = 360$

$w+x+y+z = 180$

Two opposite angles will compose of all four different variables once, so the two opposite angles will add up to $180.$

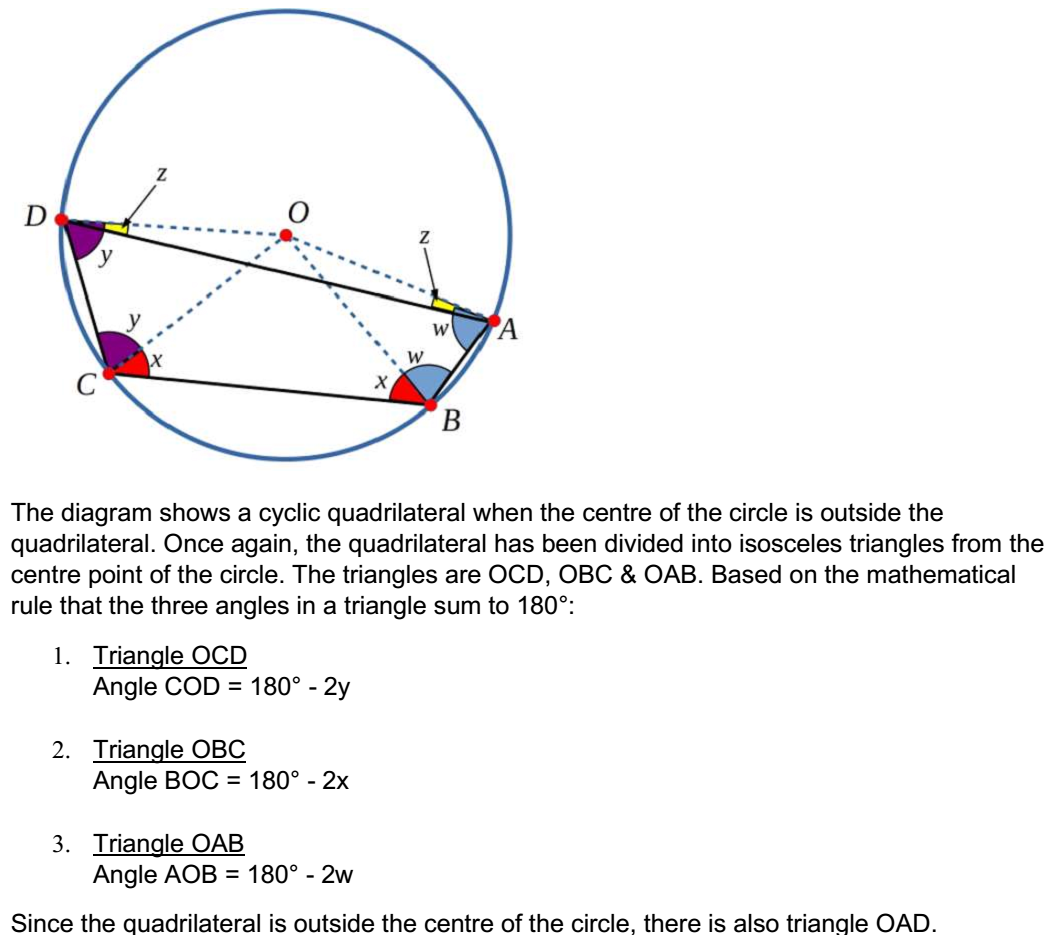
For the extension - proving that the opposite angles still add up to 180$^\circ$ even if the centre of the circle is outside the quadrilateral - Neel from Zurich International school in Switzerland sent in this example. Note that Neel has proved that it has worked for one cyclic quadrilateral, but not for all possible cyclic quadrilaterals.

This is Nayanika's proof (similar to Theo's proof above) (click on the image to see a larger version):

This is Rohan's proof (similar to Sunhari's proof above):