Amicable Arrangements

Three elves who work at Santa's factory are having a festive feast, and each one invites their best friend who works at the University of the North Pole. The three elves and their besties sit down at a round table. All of the possible seating arrangements of the six party-goers are equally likely.

(a) Show that the probability that each elf sits next to their bestie is $\frac 2 {15}$.  

A good first step is to decide on some notation. Perhaps $E_1, E_2, E_3$ for the elves and $B_1, B_2, B_3$ for the associated best friends, so that $B_1$ is the best friend of $E_1$ etc.

This is a round table, so we can use symmetry to simplify the problem a bit.  We can think of $E_1$ as being in a fixed seat, and then only have to worry about the positions of the other five party-goers.  How many ways can you arrange five people?

You might find that diagrams (like the one below) are helpful.


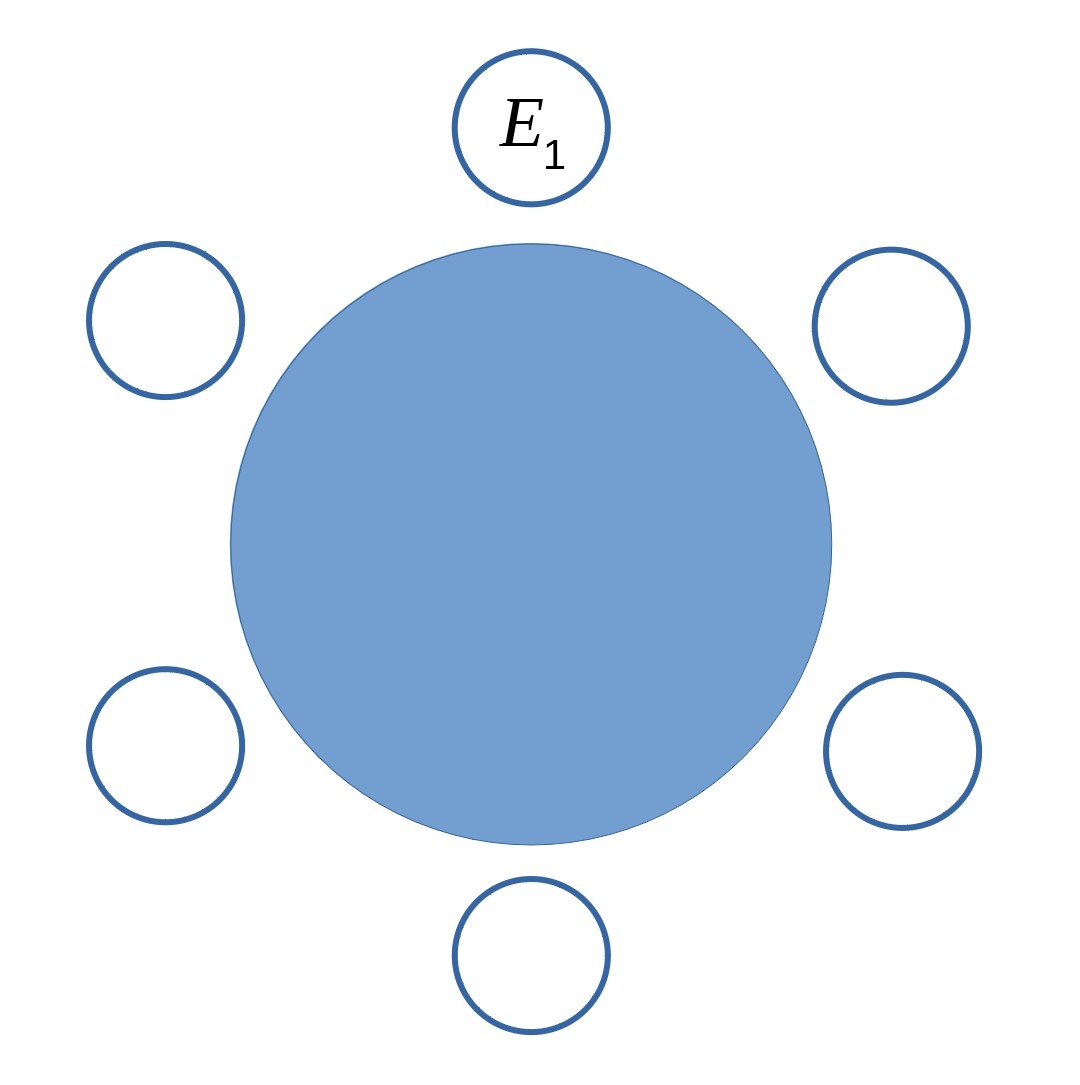
There are some more hints for this part in the Getting Started section.

(b) Find the probability that exactly two of Santa's elves sit next to their best friends.  

You can start by considering the case when $E_1$ and $B_1$ are separated (and so $E_2$ and $B_2$ sit together, and $E_3$ and $B_3$ sit together).

In the diagram below, which of the seats can $B_1$ not sit in if we are to have $E_1$ and $B_1$ separated?  Are there any seats which mean that $E_1$ and $B_1$ are separated, but we cannot sit the other four elves in two pairs?  How many seats can $B_1$ actually sit in?



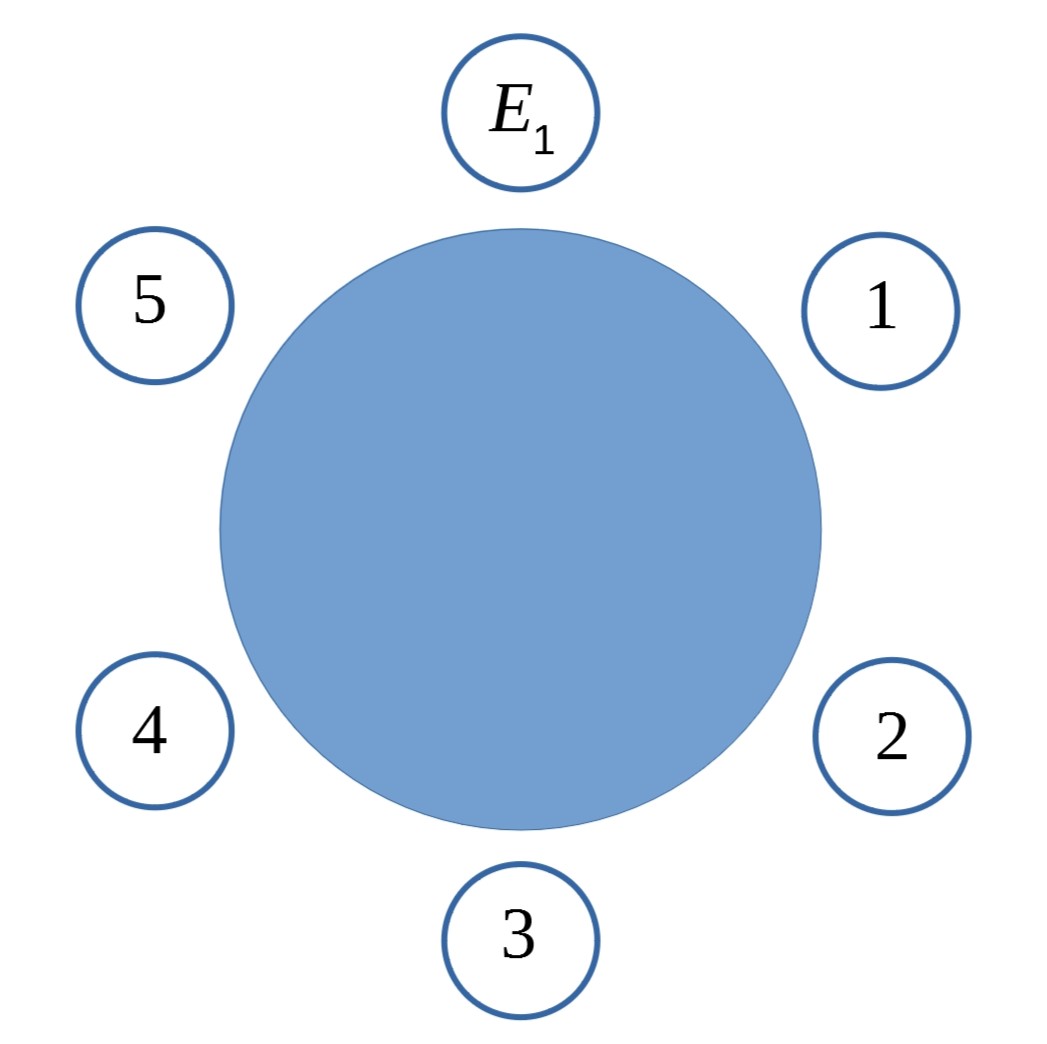
How many options are there for the other seats?  Maybe start with seat $1$?

Once you have found the number of ways of keeping $E_1$ and $B_1$ separated but the other two pairs are together, you can use symmetry to find the number of ways of keeping $E_2$ and $B_2$ or $E_3$ and $B_3$ separated.

(c) Find the probability that no elf sits next to their best friend.

Based on STEP Mathematics I, 2008, Q13. Question reproduced by kind permission of Cambridge Assessment Group Archives. The question remains Copyright University of Cambridge Local Examinations Syndicate ("UCLES"), All rights reserved.