Amicable Arrangements

Here are some further hints:

(a) Once $E_1$ is fixed you have a situation which looks like this:

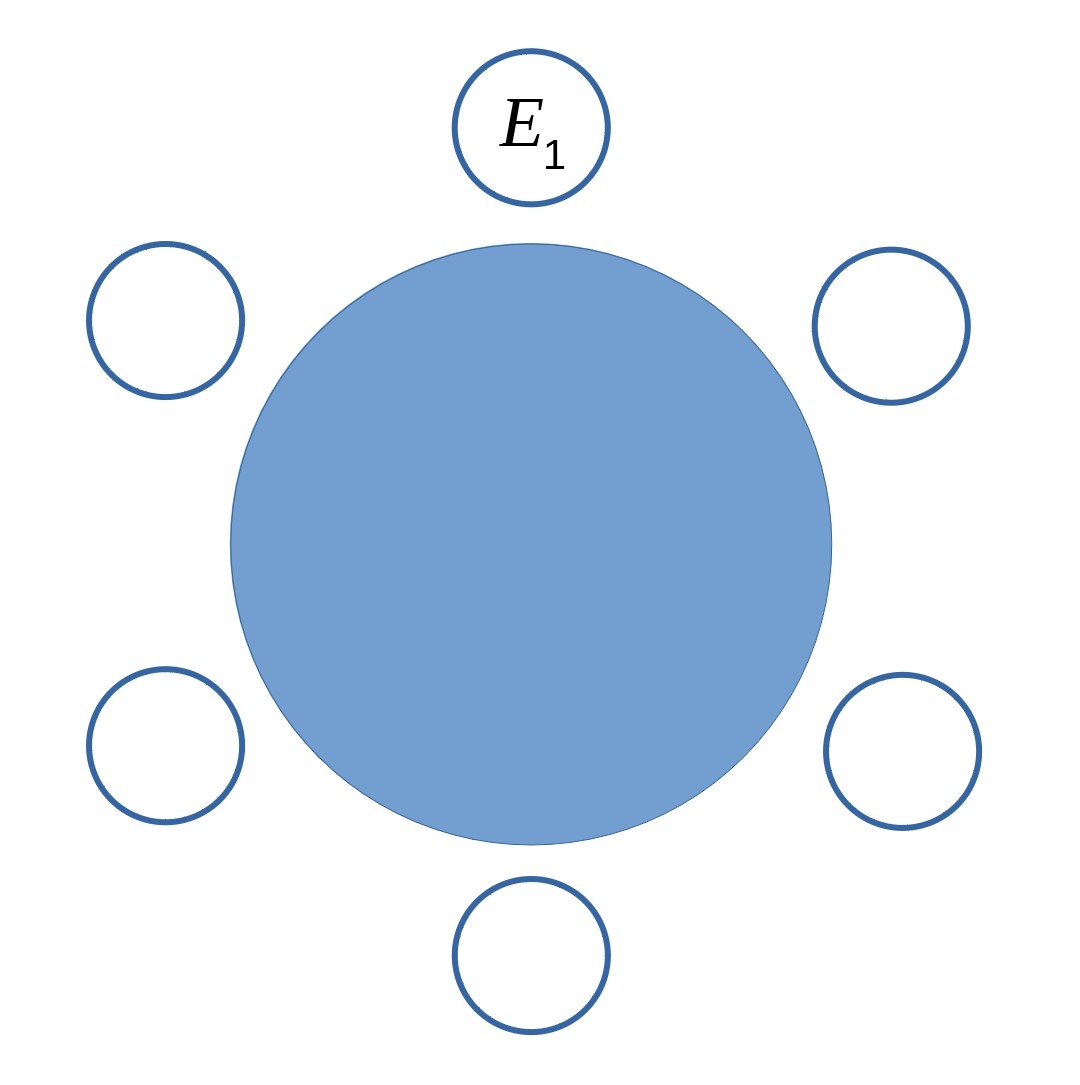
How many ways can you seat the other $5$ people?

If we need to have every elf next to their best friend, in how many different seats can $B_1$ sit?
How many choices are there for the person sitting on the other side of $E_1$?

If the $5$ other people can sit anywhere with out restriction, then there are $5$ possible seats for $B_1$, 4 possible seats for $E_2$, 3 possible seats for $B_2$ etc.  This means that there are $5 \times 4 \times 3 \times 2 \times 1 = 120$ possible arrangements.

$B_1$ can sit either to the right or the left of $E_1, as shown below:



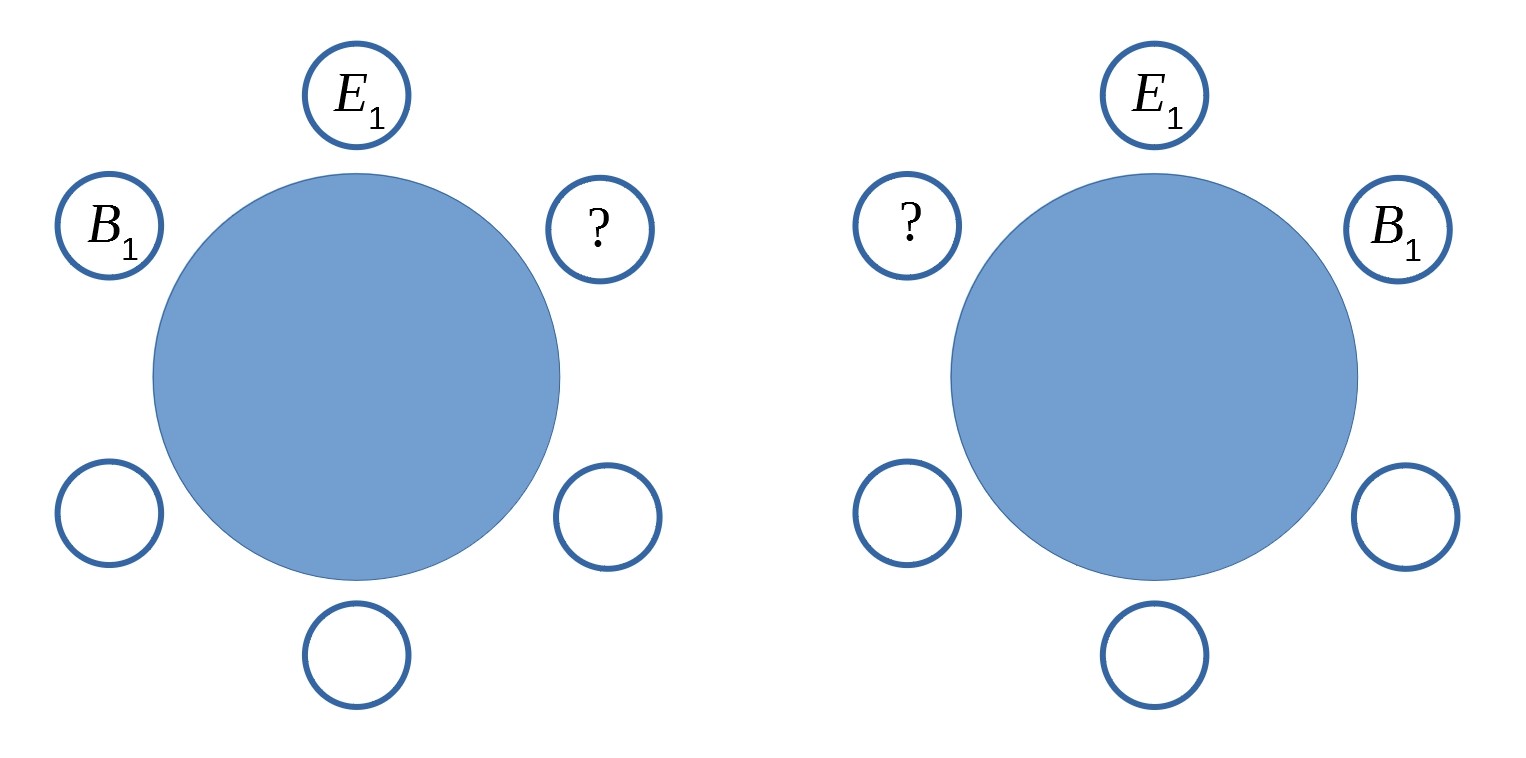
It doesn't matter who sits on the other side of $E_1$, so there are 4 possibilities for the question mark in each of the two possible places for $B_1$.

How many choices are there now for the person sitting next to the second person placed next to $E_1$?
How many ways can you fill in the last two seats?

You should now be able to calculate the total number of ways in which everyone can be sat in such a way that each elf is next to their best friend.  You also have the total number of ways in which everyone can be sat if there is no restriction.  Can you now show that the probability that each elf sits next to their best friend is $\frac 2 {15}$?