Amicable Arrangements

(a) Show that the probability that each elf sits with his bestie is $\frac2{15}.$

Anes, Jessica, Adil and Akua from London Academy of Excellence Tottenham, Isabella from King's College London Maths School, Sujay from Avanti House Secondary School, all in the UK, and Norman from Bangkok Patana School in Thailand seated the elves and besties one by one. This is Norman's work with Akua's diagrams:

There are 6 elves in total, E1, E2, E3, B1, B2, B3. If the elves are in a line (not a circle), isolating 1 elf from the list means that for example, E1 has an equal chance of sitting with either E2, E3, B1, B2, or B3. Allocating the best friend of the elf according to their number means that E1’s best friend is B1. If this is the case this means that there is a $\frac15$ chance that E1 sits with B1. [note that Norman assumes that B1 sits on our right hand side, and multiplies by 2 at the end]

If E1 is then sitting with B1, this means that E2, E3, B2, B3 are left.

There is a $\frac13$ chance that E2 will sit next to B2.

And now there is a $\frac11$ chance that E3 will sit next to E3.

Multiplying all the probabilities together will get $\frac1{15}$ that all the elves will sit next to their besties in a straight line. However, since they are sitting on a round table, the probability would double since everyone would now be sitting next to 2 others, therefore $\frac2{15}$ chance of sitting next to their bestie. [this corresponds to considering B1 on the other side of E1, and filling the table anticlockwise rather than clockwise. Akua accounted for this possibility by writing $\frac25$ rather than $\frac15$ for the first probability.]

Emily from Bishop's Wordsworth's Grammar School in the UK thought about all of the possible arrangements of elves and friends:

Adil from London Academy of Excellence Tottenham used a similar method, but pre-grouped each elf with their bestie:

Nishad from Thomas Estley Community College in the UK had a similar method but expressed it in a different way (click to enlarge):

(b) Find the probability that exactly two of Santa's elves sit next to their best friends.

Emily, Isabella and Nishad considered all of the possible arrangements. Emily used diagrams and lists. Click to see Emily's work.

Isabella, Norman, Sujay and Jessica generalised for a neater approach this is Isabella's work (click to enlarge):

Nishad used words and logic. Click to see Nishad's work.

(c) Find the probability that none of Santa's elves sit next to their best friends.

Emily listed all the possibilities again. Click to see Emily's work.

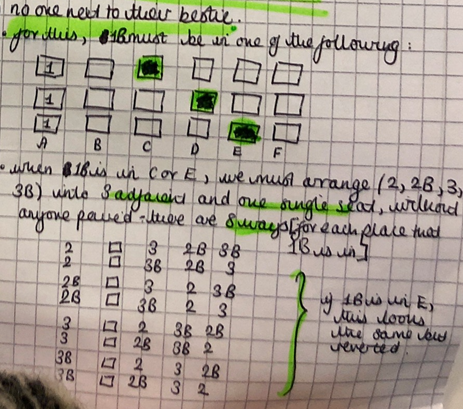
Sujay and Jessica considered the possible arrangements without drawing them all. This is Sujay's work:

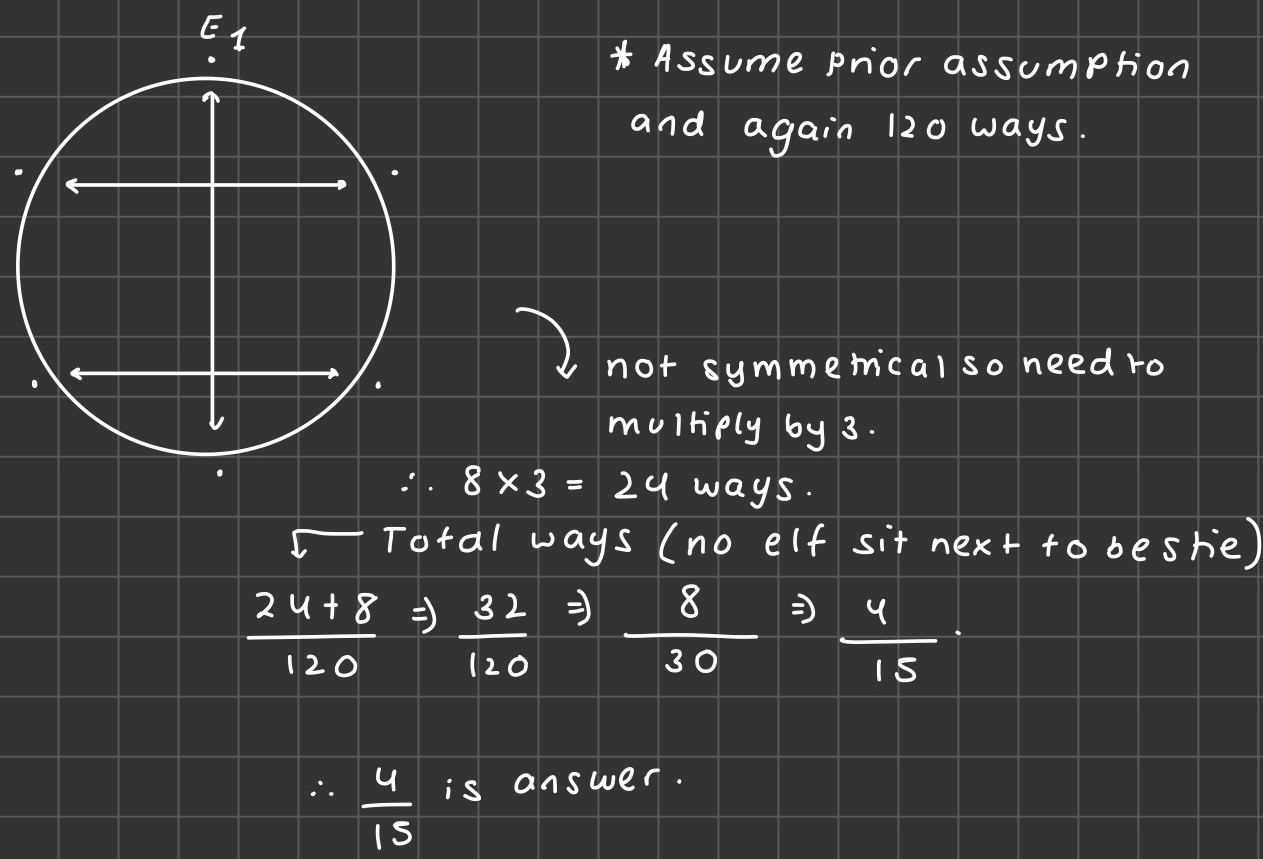
Isabella and Nishad used a process of elimination. This is Isabella's work:

Click to see Nishad's work.