Salinon

Correct solutions were received from Roy of Allerton High School, Hannah of St Helen's and St Katharines and Andre of Tudor Vianu National College, Bucharest. All used the method below. Well done to you all.

The areas are equal.




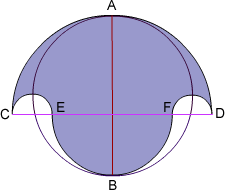
The salinon is composed of semicircles on $CD$, $EF$, $CE$ and $FD$.

Now we can find the area of the salinon in terms of these semicircles as follows;

Let the big semicircle on $CD$ have a radius of $a$, the medium one on $EF$ be radius $b$. Then the small circles on $CE$ and $FD$ have a radius of $\frac{a-b}{2}$ and the circle on $AB$ has radius $ \frac{a+b}{2}$.

The area of the semicircle on $CD$ is $ \pi \times \frac{a^2}{2}$.

The bottom semi circle (on $EF$) has an area of $ \pi \times \frac{b^2}{2}$.

The two smaller semi circles, on $CE$ and $FD$ together make a circle whose area is $ \pi \times \left(\frac{a-b}{2}\right)^2 $

The total area of the salinon is:

the top semi circle + the bottom semi circle - the two smaller identical semi circles or $$ \pi \frac{a^2}{2} + \pi \frac{b^2}{2} - \pi\left(\frac{a-b}{2}\right)^2 $$ multiplying out all the brackets you get $$ \frac{\pi}{4} \times (a^2 + b^2 + 2ab) $$

Now for the area of the main circle with diameter $AB$:

the radius of the circle is $$ \frac{a+b}{2}$$ so the area of it is $$ \pi\times \left(\frac{a+b}{2}\right)^2 $$ which, when multiplied out is the same as the area of the salinon.