Skip over navigation
Data Chunks
Age 14 to 16
Challenge Level 
Systematic working and recording of results help a lot here.
Conjectures are important, and should be encouraged, but along with a challenge to really explain why any claim might be true generally.
We hope the problem will give students a genuine pleasure in discerning real structure, and lead their interest on into Number Theory.
The articles on the NRICH site (see link from problem page) are an excellent follow-on.
You may also like
Euler's Squares
Euler found four whole numbers such that the sum of any two of the numbers is a perfect square...
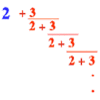
There's a Limit
Explore the continued fraction: 2+3/(2+3/(2+3/2+...)) What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?