Skip over navigation
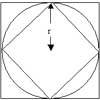
In general, if $L_n$ is the length of the spoke with $n$ spokes, $x_n$ the length of the edge of the polygon in the centre and $r_n$ the radius of the circumcircle of the polygon,then $$L_n = {x_n\over 2} + \sqrt {1 - (r_n\cos {\pi\over n})^2}$$ so that$L_n \to 1$ as $n\to \infty$.\par For $n=3$, $L_n \approx 1.595$; for $n=20$, $L_n\approx 1.011$ and for ${n=30}$, $L_n\approx 1.003$.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
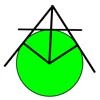
Spokes
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
|
You know what the area of the four parts must be.
Think about symmetrical drawings.
Can you draw three lines inside the circle in such a way that
they enclose an area which can be expanded or contracted to give
the required area?
The Solution section gives one possibility (see link above).
There are many other possibilities you could investigate.
Here is just one alternative line of approach you could
pursue:
The diagram shows another solution for 3 lines but the same
principle applies to any regular polygon. For an $n$-gon the angle
marked at the centre of the circle $C$ will be ${\pi \over n}$. As
$n$ gets larger the polygons will get smaller and the lines will
'radiate' out more like the spokes of a wheel.
|
In general, if $L_n$ is the length of the spoke with $n$ spokes, $x_n$ the length of the edge of the polygon in the centre and $r_n$ the radius of the circumcircle of the polygon,then $$L_n = {x_n\over 2} + \sqrt {1 - (r_n\cos {\pi\over n})^2}$$ so that$L_n \to 1$ as $n\to \infty$.\par For $n=3$, $L_n \approx 1.595$; for $n=20$, $L_n\approx 1.011$ and for ${n=30}$, $L_n\approx 1.003$.
You may also like
Mean Geometrically
A and B are two points on a circle centre O. Tangents at A and B cut at C. CO cuts the circle at D. What is the relationship between areas of ADBO, ABO and ACBO?
Approximating Pi
By inscribing a circle in a square and then a square in a circle find an approximation to pi. By using a hexagon, can you improve on the approximation?

