Skip over navigation
This challenge extends other NRICH challenges which present the same mathematical system for exploration in different ways by different groups of learners: 'Round and round the circle', Path to the stars' and Stars. In the first and last of these you will find interactivities for experimenting with these ideas. In Stars there are downloadable pdfs so you can print out circles with different numbers of equally spaced dots around the circles for paper and pencil explorations.
Celia Hoyles once said that the best mathematical problems challenge people of all ages by providing some questions that everyone can answer, and aesthetically pleasing patterns that everyone can appreciate, while at the same time leading to more challenging questions and more general conjectures which require sophisticated arguments and rigorous proofs.
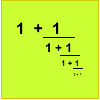

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Spirostars
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This challenge extends other NRICH challenges which present the same mathematical system for exploration in different ways by different groups of learners: 'Round and round the circle', Path to the stars' and Stars. In the first and last of these you will find interactivities for experimenting with these ideas. In Stars there are downloadable pdfs so you can print out circles with different numbers of equally spaced dots around the circles for paper and pencil explorations.
Celia Hoyles once said that the best mathematical problems challenge people of all ages by providing some questions that everyone can answer, and aesthetically pleasing patterns that everyone can appreciate, while at the same time leading to more challenging questions and more general conjectures which require sophisticated arguments and rigorous proofs.
|
Lynne McClure introduced us to the activity where, given
enough space and enough string, a whole class can stand in a circle
and the string can be passed from one person to another to form a
star.
Suppose there are $q$ people in the circle and the string is
passed to the $p$th person around the circle each time. This leads
to many questions about symmetry, about how the stars are formed,
about why the activity sometimes produces regular polygons, and
about how many different stars can be formed for a given $q$ by
varying $p$.
|
Variants of this activity are provided by using a circular
geoboard, or in
this interactivity which is a virtual geoboard, or by drawing
on a printed sheet with dots around the circumferences of
circles
All these activities presuppose that the points lie on a
circle and the angle of turn is a rational multiple of 360 degrees
and in this problem we make neither assumption.
This problem leads on to more general questions about
spirolaterals. In the question
Spiroflowers we consider what happens if the lengths of the
line segments in the path are varied and what happens if both the
lengths of the line segments and the angles of turn are
varied.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Rational Roots
Given that a, b and c are natural numbers show that if sqrt a+sqrt b is rational then it is a natural number. Extend this to 3 variables.

