Skip over navigation
Chris, who did not reveal his school, sent the following:
Working in degrees, if $\theta$ divides 360 then the shape will be a regular polygon. Else if $\theta$ is rational, the shape will be a star. If $\theta$ is irrational then a 'donut' shape will eventually be drawn, i.e. a star with infinitely many points.
Consider theta being irrational. No matter how many turns are made, the pen will never be pointing in the same direction so cannot repeat its path.
To complete the solution to this problem, consider the diagram:
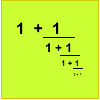

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Spirostars
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Chris, who did not reveal his school, sent the following:
Working in degrees, if $\theta$ divides 360 then the shape will be a regular polygon. Else if $\theta$ is rational, the shape will be a star. If $\theta$ is irrational then a 'donut' shape will eventually be drawn, i.e. a star with infinitely many points.
Consider theta being irrational. No matter how many turns are made, the pen will never be pointing in the same direction so cannot repeat its path.
To complete the solution to this problem, consider the diagram:
|
First think: 'why do the points lie on a circle?' We should
not take for granted that they do so we must first prove it.
Draw the perpendicular bisectors of the line segments $AB$ and
$BC$, then the intersection of the perpendicular bisectors is
equidistant from $A$, $B$ and $C$ and thus it is the centre of the
circle with $AB$ and $BC$ as chords. All the perpendicular
bisectors of the line segments in the path will meet in a single
point $O$ equidistant from the endpoints of the line segments.
Therefore all the line segments are chords of a single circle with
centre $O$.
The angle of turn between the equal chords $AB$ and $BC$ in
the path is $\angle PBC = \theta$. Triangles $AOB$ and $BOC$ are
isosceles and $\angle OAB = \angle OBA = \angle OBC = \alpha$. Then
(using angles on a straight line and angles in a triangle) $\theta
= 180 - 2\alpha = \angle AOB$.
|
Consider radii drawn from the centre to the ends of $n$
consecutive chords in the path....
Now can you prove that the path is closed if and only if
$\theta$ is a rational multiple of 360 degrees? Consider radii
drawn from the centre to the ends of $n$ consecutive chords in the
path. The sum of angles between the radii is equal to the total
angle turn $n\theta$ so the path is closed if and only if the total
angle turn is an integer multiple of 360 degrees, that is if and
only if $n\theta = 360m$ or, equivalently $\theta$ is a rational
multiple of 360 degrees.
So consider $\theta = 360 {p\over q}$ where $p$ and $q$ are
positive integers and $p< q$. If the angle of turn is more than
360 degrees, complete revolutions can be discounted, so effectively
$\theta = 360 {p*\over q }$ produces the same path as $\theta = 360
{p\over q}$ where $p* \equiv p$ mod $q$.
If $p$ is a factor of q, (say $q = kp$) then the path is a
regular $k$ sided polygon because the total angle turned when $k$
chords are drawn is $k \times {360\over k}= 360$ degrees.
If $p$ and $q$ are not coprime then $sp=tq$ for some integers
$s$ and $t$ so that the total angle turn with s chords is $s \times
360{p\over q} = 360t$ which is an integer multiple of 360 degrees
so the path is a star with $s$ points. If $p$ and $q$ are coprime
then the path is a $q$ pointed star.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Rational Roots
Given that a, b and c are natural numbers show that if sqrt a+sqrt b is rational then it is a natural number. Extend this to 3 variables.

