Skip over navigation
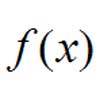
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
What Do Functions Do for Tiny X?
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This problem begins to motivate the existence of the Maclaurin's series in which any function which is well-behaved at the origin can be written as an 'infinite polynomial' or 'power series'. This iterative method is a numerical way of finding the coefficients of the polynomial, although calculus can be used in cases where the derivatives of the function needing to be approximated are known.
You may also like
Towards Maclaurin
Build series for the sine and cosine functions by adding one term at a time, alternately making the approximation too big then too small but getting ever closer.
Taking Trigonometry Series-ly
Look at the advanced way of viewing sin and cos through their power series.

