Skip over navigation
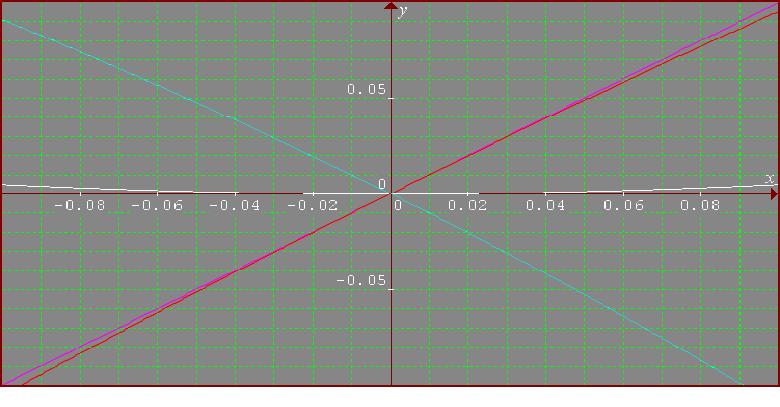
For [-0.1, 0.1]
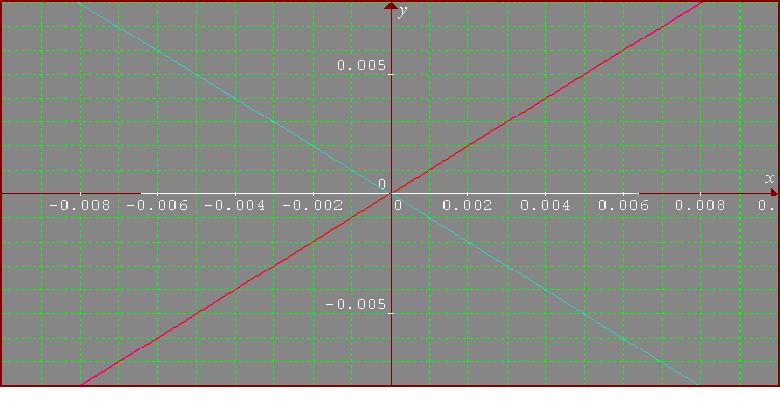
And for [-0.01, 0.01] I have:
 Each of the 4
functions could be approximated using the Taylor series expansion
around 0, and the accuracy of the approximation becomes better for
values of $x$ nearer to the origin. I shall use the second order
polynomial: $$A(x) \approx x,\quad B(x) \approx 1- (1 - x^2/2) =
x^2/2, \quad C(x)\approx x - x^2/2, \quad D(x) \approx - x -
x^2.$$
Each of the 4
functions could be approximated using the Taylor series expansion
around 0, and the accuracy of the approximation becomes better for
values of $x$ nearer to the origin. I shall use the second order
polynomial: $$A(x) \approx x,\quad B(x) \approx 1- (1 - x^2/2) =
x^2/2, \quad C(x)\approx x - x^2/2, \quad D(x) \approx - x -
x^2.$$
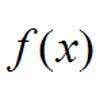
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
What Do Functions Do for Tiny X?
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Congratulations Andrei for another very good solution.
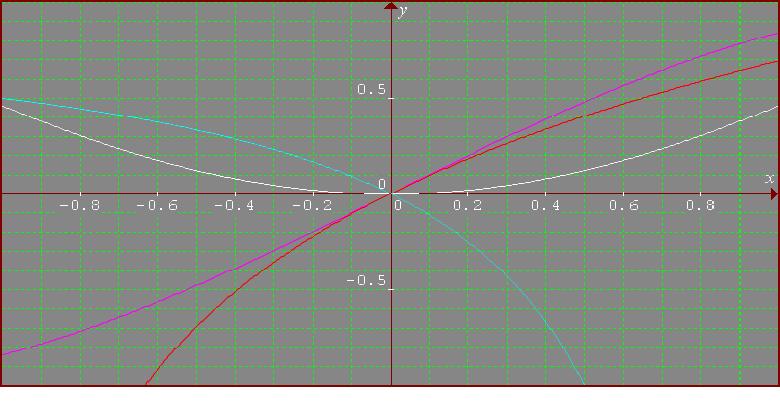
The 4 functions are: $$A(x) = \sin x,\quad B(x) = 1 - \cos x,\quad C(x) = \log (1+x), \quad D(x) = 1- {1\over (1-x)}.$$ I consider the logarithm in base e. First I plotted the 4 functions using Graphmatica. In all figures $A(x)$ is violet, $B(x)$ is white, $C(x)$ is red and $D(x)$ is cyan. For $[-1, 1]$ I obtain:
For [-0.1, 0.1]
And for [-0.01, 0.01] I have:
You may also like
Towards Maclaurin
Build series for the sine and cosine functions by adding one term at a time, alternately making the approximation too big then too small but getting ever closer.
Taking Trigonometry Series-ly
Look at the advanced way of viewing sin and cos through their power series.

