Skip over navigation

Partly Circles

Age 14 to 16

Challenge Level Yellow star

Secondary curriculum

Partly Circles printable sheet

Here are three problems involving circles.

Can you solve them?
Can you find relationships between the three problems?

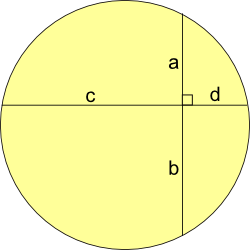
Firstly Show that ab = cd (where a, b, c, d are lengths)

A circle, with two chords that intersect at right angles, dividing one chord into lengths a and b, and the other into lengths c and d

Secondly:

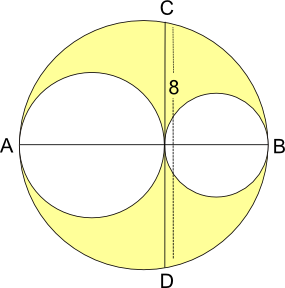
These three circles are drawn so that they touch each other, and their centres are all on the line AB.

If CD is $8$ units in length, what is the area of the region shaded yellow?

A yellow circle with diameter AB. Two white circles are drawn over it, with their centres on AB, so their diameters add up to the total length. CD is a chord of length 8 which is tangent to the two white circles.

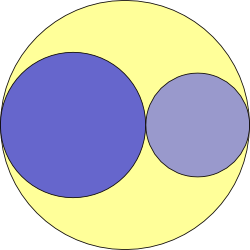
Lastly: If the area shaded yellow is equal to the area of the larger of the two blue circles, what is the relationship between the radii of the three circles?

A yellow circle with two circles drawn inside so the two circles are tangent to each other and to the outer circle, with their centres all on the same line.

The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ

Look Before You Leap

Can you spot a cunning way to work out the missing length?

Triangle Midpoints

You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Partly Circles

You may also like

Fitting In

Look Before You Leap

Triangle Midpoints