Skip over navigation
Well done to all those who sent in solutions to parts of this problem. We received a very clear and full explanation to all three parts of the problem from Daniel at Savile Park School, which you can see below:
Firstly:
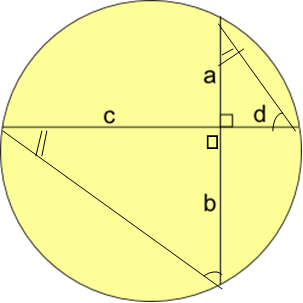
Join a to d, and b to c, to make two triangles. These triangles are similar because they have identical angles (angles in the same segment are equal).
So $ {a}\over{c}$ $=$ ${d}\over{b}$, which rearranges to give
$ab = cd$.
Daniel spotted that we do not need any numerical information to find a connection between the lengths, all we need to notice is that the triangles are similar!
Secondly:
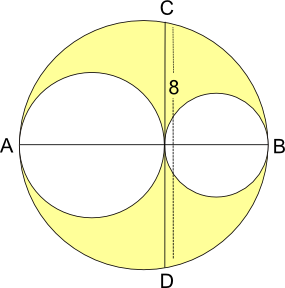
Yellow Area $=$ Area of big circle $-$ Area of two smaller circles
Let the radius of the smaller circle be $r$, and the next circle be $R$. Then the radius of the big circle is $r+R$.
Yellow Area $=\pi (r+R)^2 - \pi r^2 - \pi R^2$
$=\pi ((r^2+2rR+R^2)-r^2-R^2)$
$=2\pi rR$
Using the result from the first part, if CD is halved, the product of the two halves is equal to the product of the diameters of the two smaller circles, so
$2r \times 2R = 4 \times 4$
$4rR = 16$
$rR = 4$.
But we know the yellow area is $2\pi rR$, so the yellow area must be $8\pi$.
Thirdly:
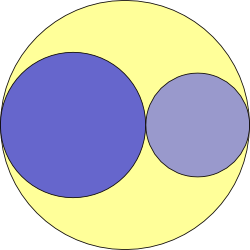
If the yellow area is equal to the larger of the two blue circles, we have
$\pi R^2 = 2\pi rR$
$R = 2r$
so the radius of the yellow circle is $r+2r=3r$
so the radii are in the ratio $1:2:3$.
To solve the second part of the problem, Daniel needed to take the step of working with algebra to find relationships. He then spotted that he could use the first part of the question to help him to an answer. The third part involved equating the area of the larger blue circle to the formula he had just found for the yellow area. Well done Daniel!
Partly Circles
Age 14 to 16
Challenge Level 
Well done to all those who sent in solutions to parts of this problem. We received a very clear and full explanation to all three parts of the problem from Daniel at Savile Park School, which you can see below:
Firstly:
Join a to d, and b to c, to make two triangles. These triangles are similar because they have identical angles (angles in the same segment are equal).
So $ {a}\over{c}$ $=$ ${d}\over{b}$, which rearranges to give
$ab = cd$.
Daniel spotted that we do not need any numerical information to find a connection between the lengths, all we need to notice is that the triangles are similar!
Secondly:
Yellow Area $=$ Area of big circle $-$ Area of two smaller circles
Let the radius of the smaller circle be $r$, and the next circle be $R$. Then the radius of the big circle is $r+R$.
Yellow Area $=\pi (r+R)^2 - \pi r^2 - \pi R^2$
$=\pi ((r^2+2rR+R^2)-r^2-R^2)$
$=2\pi rR$
Using the result from the first part, if CD is halved, the product of the two halves is equal to the product of the diameters of the two smaller circles, so
$2r \times 2R = 4 \times 4$
$4rR = 16$
$rR = 4$.
But we know the yellow area is $2\pi rR$, so the yellow area must be $8\pi$.
Thirdly:
If the yellow area is equal to the larger of the two blue circles, we have
$\pi R^2 = 2\pi rR$
$R = 2r$
so the radius of the yellow circle is $r+2r=3r$
so the radii are in the ratio $1:2:3$.
To solve the second part of the problem, Daniel needed to take the step of working with algebra to find relationships. He then spotted that he could use the first part of the question to help him to an answer. The third part involved equating the area of the larger blue circle to the formula he had just found for the yellow area. Well done Daniel!
You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?