Ford Circles

Why do this problem?

This problem provides a beautiful extension to Farey Neighbours and encourages students to explore the connection between a geometrical pattern and a numerical sequence.

Possible approach

It would be helpful if students were familiar with Farey Sequences and Farey Neighbours.
Start by demonstrating the first GeoGebra applet and defining Ford Circles: 
"Ford Circles have centre $\left(\frac{p}{q},\frac1{2q^2}\right)$ and radius $\frac1{2q^2}$, where $\frac{p}{q}$ is a fraction in its simplest form (that is, $p$ and $q$ are coprime integers)."

Invite students to explore the second GeoGebra applet and challenge them to find some values of $a, b, c$ and $d$ that generate circles which touch. Record any that they find, and invite them to look for patterns, drawing attention to $ad-bc$ if it does not emerge from the class.

The two questions at the end of the problem are the key to the link between Ford Circles and Farey Sequences, and provide a good challenge in proof for older students:

• Can you prove that for any touching circles in the interactivity, $|ad-bc|=1$
• Can you prove that, given two such circles which touch the $x$ axis at $\frac bd$ and $\frac ac$, the circle with centre $\left(\frac{a+b}{c+d},\frac1{2(c+d)^2}\right)$ and radius $\frac1{2(c+d)^2}$ is tangent to both circles?

A diagram like this one might help:


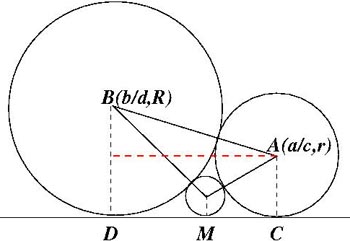
$R=\frac{1}{2d^2}$ and $r=\frac{1}{2c^2}$.
The centre of the circle which touches the horizontal axis at $M$ is $(\frac{a+b}{c+d}, \frac{1}{2(c+d)^2})$.

Key questions

What can you say about $R+r$ and $R-r$ if the circles centre $B$ and $A$ just touch each other?
Can you use Pythagoras theorem? 

Possible extension

Students may wish to read more about Ford Circles in this Wikipedia article.
 

Possible support

As well as working on Farey Neighbours, Baby Circle would be a useful problem to try before attempting this challenging task.