Skip over navigation
1a) During one round of PCR, the DNA double helix is separated into its constituent strands, and new strands are built up against each of these. The final products are two helices, and so the DNA content of the cell doubles.
b) If there is originally 1mg of DNA in the sample, 30 rounds of PCR, will lead to doubling thirty times:
$Mass_{final} = 0.001 \times 2^{15} = 32.8$g of DNA
c) We must first calculate the number of moles of DNA in the sample:
$Moles = \text{concentration} \times \text{volume} = 0.1 \times 10^{-12} \times 0.5 \times 10^{-3} = 5 \times 10^{-17}$ moles DNA
The number of molecules of DNA is calculated by multiplying moles by Avogadro's number:
$Molecules = 5 \times 10^{-17} \times 6.02 \times 10^{23} = 3.01 \times 10^7$
Thus to work out the number of rounds of PCR necessary:
$3.01 \times 10^7 \times 2^n = 10^{12}$
$2^n = \frac{10^{12}}{3.01 \times 10^7}$
$n = \frac{ln(\frac{10^{12}}{3.01 \times 10^7})}{ln(2)} = 15.02$
Therefore, we require 16 rounds of PCR to exceed $10^{12}$ molecules of DNA.
2a) Number of minutes = $\frac{24000}{6000} = 4$
b) In the first round of PCR, we will incorporate $2 \times 24000 = 48000$ bases into DNA. In the next round there will be four template strands, and so $4 \times 24000 = 96000$ bases will be incorporated into DNA. Thus over a total of ten rounds:
Number of incorporated bases = $ 24000 \times ( 2^1 + 2^2 +2^3 +...+2^{10})$
The part in brackets is a geometric series, which can be summed as follows:
Let $ x = 2^1 + 2^2 +2^3 +...+2^{10}$
Then $2x = 2^2 +2^3 +2^4 +...+2^{11}$
$\therefore 2x -x = 2^{11} - 2$
$\rightarrow x = 2^{11} -2= 2(2^{10} - 1)$
Thus, the number of incorporated bases = $24000 \times 2(2^{10} -1)= 48000(2^{10} -1) = 4.91 \times 10^7$
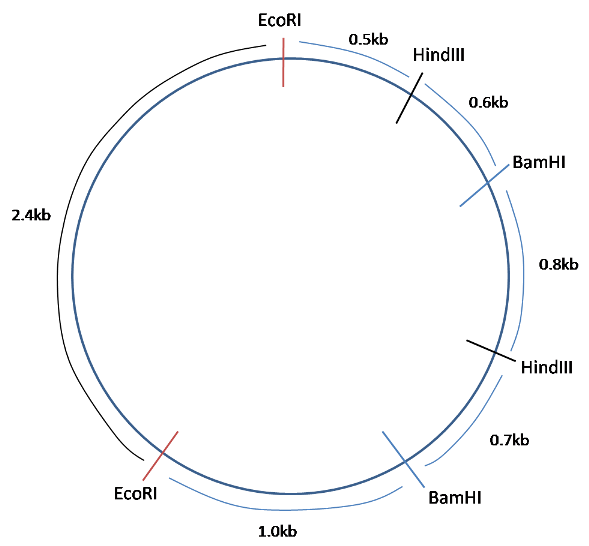
3) Solving the restriction map is done by partly by trial and error, and partly by building the map up with more and more information until the solution is found:

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Why Multiply When You're about to Divide?
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
1a) During one round of PCR, the DNA double helix is separated into its constituent strands, and new strands are built up against each of these. The final products are two helices, and so the DNA content of the cell doubles.
b) If there is originally 1mg of DNA in the sample, 30 rounds of PCR, will lead to doubling thirty times:
$Mass_{final} = 0.001 \times 2^{15} = 32.8$g of DNA
c) We must first calculate the number of moles of DNA in the sample:
$Moles = \text{concentration} \times \text{volume} = 0.1 \times 10^{-12} \times 0.5 \times 10^{-3} = 5 \times 10^{-17}$ moles DNA
The number of molecules of DNA is calculated by multiplying moles by Avogadro's number:
$Molecules = 5 \times 10^{-17} \times 6.02 \times 10^{23} = 3.01 \times 10^7$
Thus to work out the number of rounds of PCR necessary:
$3.01 \times 10^7 \times 2^n = 10^{12}$
$2^n = \frac{10^{12}}{3.01 \times 10^7}$
$n = \frac{ln(\frac{10^{12}}{3.01 \times 10^7})}{ln(2)} = 15.02$
Therefore, we require 16 rounds of PCR to exceed $10^{12}$ molecules of DNA.
2a) Number of minutes = $\frac{24000}{6000} = 4$
b) In the first round of PCR, we will incorporate $2 \times 24000 = 48000$ bases into DNA. In the next round there will be four template strands, and so $4 \times 24000 = 96000$ bases will be incorporated into DNA. Thus over a total of ten rounds:
Number of incorporated bases = $ 24000 \times ( 2^1 + 2^2 +2^3 +...+2^{10})$
The part in brackets is a geometric series, which can be summed as follows:
Let $ x = 2^1 + 2^2 +2^3 +...+2^{10}$
Then $2x = 2^2 +2^3 +2^4 +...+2^{11}$
$\therefore 2x -x = 2^{11} - 2$
$\rightarrow x = 2^{11} -2= 2(2^{10} - 1)$
Thus, the number of incorporated bases = $24000 \times 2(2^{10} -1)= 48000(2^{10} -1) = 4.91 \times 10^7$
3) Solving the restriction map is done by partly by trial and error, and partly by building the map up with more and more information until the solution is found:

You may also like
bioNRICH
bioNRICH is the area of the stemNRICH site devoted to the mathematics underlying the study of the biological sciences, designed to help develop the mathematics required to get the most from your study of biology at A-level and university.
Catalyse That!
Can you work out how to produce the right amount of chemical in a temperature-dependent reaction?

