The Wheatstone Bridge
The circuit below is known as a Wheatstone bridge, a device popularized by Sir Charles Wheatstone. The purpose of the Wheatstone bridge is to measure some unknown impedance. This is achieved by 'balancing' the two legs of bridge, one will contain a variable resistor and the other the component whose impedance we wish to measure.
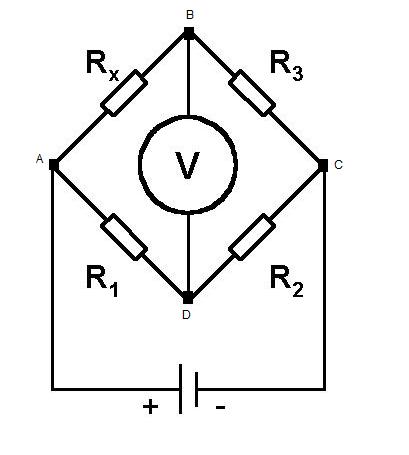
Can you find the condition on the variable resistor needed for balance ($V = 0$) using loop current analysis?
Can you find the condition for balance using a potential divider argument?
Extension:
If we now replace the DC voltage source with an AC voltage source of frequency $f$, add a capacitor $C_3$ in series with $R_3$ and added a second capacitor $C_2$ in parallel with $R_2$, at what frequency will balance occur, in terms of $R_1,R_2,C_2,R_3,C_3$ and $R_x$?
You may also like
Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built without mortar on a flat horizontal surface, to overhang by 1 metre? How big an overhang is it possible to make like this?
Stonehenge
Explain why, when moving heavy objects on rollers, the object moves twice as fast as the rollers. Try a similar experiment yourself.
Maximum Flow
Given the graph of a supply network and the maximum capacity for flow in each section find the maximum flow across the network.