Skip over navigation
We can solve the problem using a potential divider or using loop currents.
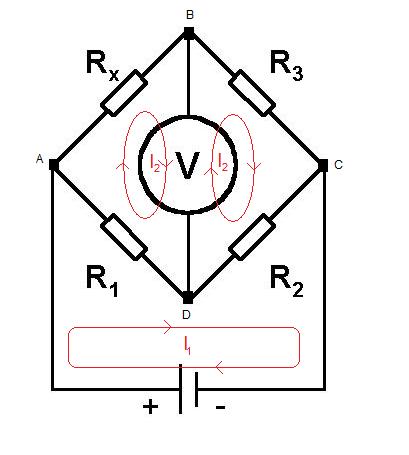
Loop Currents:
We can assign loop currents to each loop as shown above. At balance the vector sum of the currents through the meter will be zero, we can therefore assign $I_2$to both the left and right loop, the currents will cancel through the meter.
Applying Kirchoff's voltage law to each loop we find that:
$\sum_{Voltages} Left Hand Loop = - (I_2 - I_1)R_1 - I_2 R_x = 0 $
$\sum_{Voltages}Right Hand Loop = -I_2 R_3 -(I_2 - I_1)R_2 = 0 $
We have two independent equations and two unknowns ($I_1$ and $I_2$).
From the left loop: $I_2 = \frac{R_1}{R_1 + R_x} I_1$
From the right loop: $I_2 = \frac{R_2}{R_3 + R_2} I_1$
Equating we see:
$R_1R_3 = R_2R_x$
Potential Divider:
At balance $V_b = V_d$
The potential at C is zero (ground). The potential at A is therefore divided between $R_x$ and $R_3$, in addition it is also divided between $R_1$and $R_2$ .
By potential divider:
$V_b = \frac{R_3}{R_x} V_a$
$V_d = \frac{R_2}{R_1}V_a$
Equating $V_b$ and $V_d$
$R_1 R_3 = R_2 R_x$
Extension:
If we replace:
$R_2 = Z_2$
We find $Z_2$ by combing the impedance of $C_2$ in parallel with $R_2$
$Z_2= \frac{R_2 \frac{1}{2 \pi f t C \bf i}} {R_2 + 2 \pi f t C \bf i }$
where $i = \sqrt{-1} = i$
$R_3 = Z_3 = $
We find $Z_3$ by combining the imperdance of $C_3$ in series with $R_3$
where $i = \sqrt{-1} = i$
From part 1 we know that:
$R_1Z_3 = Z_2R_x$
Substituting $Z_3$, $Z_4$ and equating real and imaginary terms we find that:
the real part tells us nothing about frequency (cancels)
The imaginary part tells us f = $\frac{1}{2 \pi} \sqrt{\frac{1}{C_3 C_2 R_3 R_2}} $ at balance


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Wheatstone Bridge
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
We can solve the problem using a potential divider or using loop currents.

Loop Currents:
We can assign loop currents to each loop as shown above. At balance the vector sum of the currents through the meter will be zero, we can therefore assign $I_2$to both the left and right loop, the currents will cancel through the meter.
Applying Kirchoff's voltage law to each loop we find that:
$\sum_{Voltages} Left Hand Loop = - (I_2 - I_1)R_1 - I_2 R_x = 0 $
$\sum_{Voltages}Right Hand Loop = -I_2 R_3 -(I_2 - I_1)R_2 = 0 $
We have two independent equations and two unknowns ($I_1$ and $I_2$).
From the left loop: $I_2 = \frac{R_1}{R_1 + R_x} I_1$
From the right loop: $I_2 = \frac{R_2}{R_3 + R_2} I_1$
Equating we see:
$R_1R_3 = R_2R_x$
Potential Divider:
At balance $V_b = V_d$
The potential at C is zero (ground). The potential at A is therefore divided between $R_x$ and $R_3$, in addition it is also divided between $R_1$and $R_2$ .
By potential divider:
$V_b = \frac{R_3}{R_x} V_a$
$V_d = \frac{R_2}{R_1}V_a$
Equating $V_b$ and $V_d$
$R_1 R_3 = R_2 R_x$
Extension:
If we replace:
$R_2 = Z_2$
We find $Z_2$ by combing the impedance of $C_2$ in parallel with $R_2$
$Z_2= \frac{R_2 \frac{1}{2 \pi f t C \bf i}} {R_2 + 2 \pi f t C \bf i }$
where $i = \sqrt{-1} = i$
$R_3 = Z_3 = $
We find $Z_3$ by combining the imperdance of $C_3$ in series with $R_3$
where $i = \sqrt{-1} = i$
From part 1 we know that:
$R_1Z_3 = Z_2R_x$
Substituting $Z_3$, $Z_4$ and equating real and imaginary terms we find that:
the real part tells us nothing about frequency (cancels)
The imaginary part tells us f = $\frac{1}{2 \pi} \sqrt{\frac{1}{C_3 C_2 R_3 R_2}} $ at balance
You may also like
Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built without mortar on a flat horizontal surface, to overhang by 1 metre? How big an overhang is it possible to make like this?
Stonehenge
Explain why, when moving heavy objects on rollers, the object moves twice as fast as the rollers. Try a similar experiment yourself.
Maximum Flow
Given the graph of a supply network and the maximum capacity for flow in each section find the maximum flow across the network.

