Skip over navigation
Pour 1^{ère} cycle du secondaire
Mise en situation A
Jos s'est mis à jouer avec des paires de nombre composées de 2 chiffres. Il a plus particulièrement regardé les différences de carrés.
Jos a obtenu les résultats suivants :
Ceci l'a surpris.
Exploration
Peux-tu trouver d'autres pairs dont la différence de carrés est égale à un multiple de 1000? Que remarques-tu de spécial chez ces paires de nombre ?
Mise en situation B
Jos a aussi été surpris par les réponses suivantes:
Exploration
Peux-tu trouver d'autres paires de nombres dont la différence donne des chiffres qui se répètent ? Que remarques-tu de spécial chez ces paires de nombre?
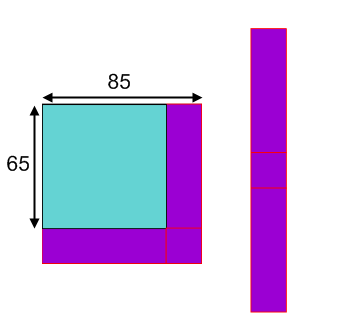
Jos veut expliquer pourquoi il a obtenu ces résultats surprenants. Il a dessiné quelques diagrammes pour l'aider. Voici le diagramme montrant 85^2 - 65^2 :
Questions
Quelle est la connexion entre le diagramme de Jos et le calcul de 85^2 - 65^2 ?
Comment est-ce que Jos peut calculer l'aire du long rectangle mauve (sans calculatrice) ?
Peux-tu dessiner des diagrammes semblables pour les autres calculs de Jos (ou pour vos propres exemples) ?
Comment est-ce que ces diagrammes ont pu aider Jos à développer une méthode rapide pour évaluer a^2 - b^2 pour n'importe quelle valeur de a et de b ?
Fais le calcul suivant sans l'aide d'une calculatrice :
7778^2 - 2233^2
88889^2 - 11112^2
Extension
Peux-tu écrire 1000, 2000, 3000 sous forme d'une différence de deux nombres carrés? Y a-t-il plus qu'une façon ?
Peux-tu écrire des nombres 1111, 2222, 3333, ... sous forme d'une différence de deux nombres carrés ?
Peux-tu le faire avec 434343, 123321, 123456, ... ?
Source: Plus Minus
Translated by Renée Michaud, Coordonnatrice et consultante de mathématiques et sciences, Consortium provincial francophone pour le perfectionnement professionnel, Calgary, Canada
Plus Ou Moins
Age 14 to 16
Challenge Level 
Pour 1^{ère} cycle du secondaire
Mise en situation A
Jos s'est mis à jouer avec des paires de nombre composées de 2 chiffres. Il a plus particulièrement regardé les différences de carrés.
Jos a obtenu les résultats suivants :
65^2 - 35^2 = 3000
55^2 - 45^2 = 1000
85^2 - 65^2 = 3000
Ceci l'a surpris.
Exploration
Peux-tu trouver d'autres pairs dont la différence de carrés est égale à un multiple de 1000? Que remarques-tu de spécial chez ces paires de nombre ?
Mise en situation B
Jos a aussi été surpris par les réponses suivantes:
89^2 - 12^2 = 7777
78^2 - 23^2 = 5555
Exploration
Peux-tu trouver d'autres paires de nombres dont la différence donne des chiffres qui se répètent ? Que remarques-tu de spécial chez ces paires de nombre?
Jos veut expliquer pourquoi il a obtenu ces résultats surprenants. Il a dessiné quelques diagrammes pour l'aider. Voici le diagramme montrant 85^2 - 65^2 :
Questions
Quelle est la connexion entre le diagramme de Jos et le calcul de 85^2 - 65^2 ?
Comment est-ce que Jos peut calculer l'aire du long rectangle mauve (sans calculatrice) ?
Peux-tu dessiner des diagrammes semblables pour les autres calculs de Jos (ou pour vos propres exemples) ?
Comment est-ce que ces diagrammes ont pu aider Jos à développer une méthode rapide pour évaluer a^2 - b^2 pour n'importe quelle valeur de a et de b ?
Fais le calcul suivant sans l'aide d'une calculatrice :
7778^2 - 2233^2
88889^2 - 11112^2
Extension
Peux-tu écrire 1000, 2000, 3000 sous forme d'une différence de deux nombres carrés? Y a-t-il plus qu'une façon ?
Peux-tu écrire des nombres 1111, 2222, 3333, ... sous forme d'une différence de deux nombres carrés ?
Peux-tu le faire avec 434343, 123321, 123456, ... ?
Source: Plus Minus
Translated by Renée Michaud, Coordonnatrice et consultante de mathématiques et sciences, Consortium provincial francophone pour le perfectionnement professionnel, Calgary, Canada
