Secret Transmissions

Why do this problem?

This problem introduces the important idea of error detection and correction from the field of Information Theory, which has applications in Computer Science.

Possible approach

Begin by introducing the compass wheel and explaining the problem:
"Agent X needs to transmit that the enemy were travelling North East, but she knows that one of the digits might be flipped in transmission, from a 1 to a 0, or vice versa. Talk to your partner and see whether you can come up with any ways she could send her base camp some extra information to ensure the message gets through."

Possible suggestions that might emerge are sending the message multiple times, or perhaps sending a check digit.

Then introduce the idea of check digits:

"Agent X decides to add one extra digit to the end so that the message always contains an even number of 1s. She claims that if at most one digit is incorrect (which could be the check digit), it is always possible for her team to tell if the message is correct or not. Is she right?"

Allow some time for discussion. Then give students the following nine messages with check digits and ask them to work out which are error-free, and how many different possible starting messages there are for those which include an error:

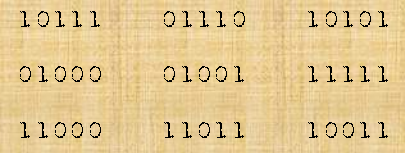
Next, hand out this worksheet.

"A single check digit can only tell us if there has been an error, but not what the error is. Here is a system of three check digits that Agent X claims can be used to detect AND correct an error in her message, as long as there is no more than one."

Give students time to make sense of the check digit system in small groups and to have a go at recreating the correct messages for the four transmissions on the sheet.

"Decide on a direction to send, and work out the three check digits. Then swap with your partner, after making a change to one of the seven digits. Can they work out what your message should say?"

Finally, allow some time to discuss how and why the check digit system allows error detection AND correction for any message with at most one error. The hint shows a diagram that may help students to make sense of how the check digits interact.

Key questions

If digit a is changed from a 1 to a 0, what is the effect on xabd, yacd, and zbcd?
What if digit b, c or d is changed?
What if digit x, y or z is changed?

 

Possible extension

More Secret Transmissions invites students to consider an error detection and correction system for longer strings of binary digits.

Possible support

This worksheet contains a couple of examples showing how Agent X's code works.

For a simpler introduction to the ideas of error detection, see Book Codes which looks at ISBN codes.