Escape from the Castle
Escape from the Castle
Skippy and Anna are imprisoned in a castle and need to find their way out of five locked rooms to escape.
To unlock each room, they need to find the solution to a problem. In each case, the solution provides the key to that room.
Can you help them to get out?
The first room:
There is a pile of dice.
Three of them are put in a row. The numbers on the top of these three add to 8.
What do the hidden numbers on the bottom add to?
This number is the first key.
The second room:
Skippy and Anna have the first key number. They have gone through the first locked door.
There are ten cards numbered from 0 to 9. Five of these are face down in a row on the table.
The numbers on the first two cards add to the first key number.
The numbers on the second and third cards add to 9.
The numbers on the third and fourth cards add to 11.
The numbers on the fourth and fifth cards add to 16.
What number is on the last card? This number is the second key.
The third room:
Skippy and Anna have the second key number. They have gone through the second locked door. Here there is a diagram.
There are two overlapping circles inside a rectangle. The rectangle is the second key number of centimetres long and 5 centimetres high.
How far apart are the centres of the two circles?
Square this answer and subtract one. This will give you the third key number.
The fourth room:
Skippy and Anna have the third key number. They have gone through the third locked door.
On the floor there is a strange diagram and the numbers from 1 to 8 on eight cards. The diagram is a square with eight boxes arranged round it.
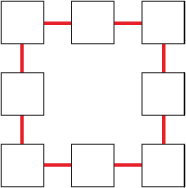
Skippy and Anna have to arrange the numbers in the boxes so that each side of the square adds to the third key number.
To find the fourth key number, add the numbers on all the corner boxes and then subtract 10.
The fifth room:
Skippy and Anna have the fourth key number. They have gone through the fourth locked door.
On the table there are some jam tarts.
The tarts were baked in two identical trays. The trays hold the fourth key number of tarts each.
There are enough tarts to fill one tray but not enough to fill the other one as well.
If the tarts are counted in fours there are three left over.
If they are counted in threes there is one left over.
How many tarts are there altogether? This number is the fifth and last key.
The last question:
Before they can leave the castle you must answer a last question.
What is Skippy's real name?
Using the code 1 = A, 2 = B, 3 = C, ... 26 = Z translate all the key numbers into letters.
These letters will give you an anagram of Skippy's real name. When you have worked this out, Skippy and Anna will be free!
Why do this problem?
This activity is really a series of connected problems. Learners will find that they must complete one part before attempting the next. From each part a 'key' number will be discovered which is required to do the next part of the problem. Accuracy and perseverance will be necessary!
Possible approach
You can download these sheets which divide the problem into its five constituent parts.
You could start by setting the scene and explaining that each part of the challenge 'feeds into' the next. Hand out the first sheet and step back. It would be best for learners to work in pairs so that they are able to talk through their ideas with a partner. When they think they have the first key number, a pair can request the next sheet and so on. You may decide not to give them feedback after each part so that if they reach a sticking point, they will have to check over what they have done so far.
Access to dice, numbered cards $(0 - 9)$ and counters will help some learners tackle the problems.
Allow time for the whole group to come together to discuss their findings and difficulties.
You may like to have a go at this digital escape room, created by Elizabeth Joyce, from Pinellas County Schools in Florida, which changes the story but includes the same mathematics.
Key questions
What do you know/what can you discover about opposite faces of a dice?
How will you record what you're doing?
Tell me about what you've done so far.
Have you thought of using numbered cards/dice/counters ...?
Possible extension
Learners could make up a similar 'story problem' for others to do.
Possible support
Encourage learners to use real dice, numbered cards, counters and anything else they think might be helpful.
You may also like
Junior Frogs
Have a go at this well-known challenge. Can you swap the frogs and toads in as few slides and jumps as possible?
Inky Cube
This cube has ink on each face which leaves marks on paper as it is rolled. Can you work out what is on each face and the route it has taken?
Area and Perimeter
What can you say about these shapes? This problem challenges you to create shapes with different areas and perimeters.