Escape from the Castle

We were overwhelmed with solutions for this problem - thank you everyone.  Many of you sent good explanations for each part.

Daniel from Kings School, New Zealand sent a very clear solution:

The First Room:

To solve this room, you must know that opposite sides of a dice always add up to seven. For example, if someone puts a dice on the floor and asks what number is on the other side, you can immediately tell them that the number is six if the number on the top of the die is one.

Since all opposite sides add up to seven, you must multiply seven by the number of dice there were (three). Because the sum of the numbers on the top of the dice is eight, you must subtract $8$ from $21$ to reveal the sum of the numbers that you can't see.

The key to the first room is 13.

The Second Room:

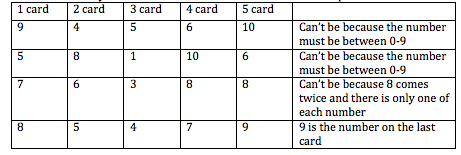
The first card is $8$.

The second card is $5$.

The third card is $4$.

The fourth card is $7$.

The fifth card is $9$.

First card and second card add up to $13$ (key to the first room). Second and third card add up to $9$. Third card and fourth card add up to $11$. Fourth card and fifth card add up to $16$.

The key to the second room is $9$.

The Third Room:

The diameter of the circle is $5$cm. Halve this to get the radius ($2.5$cm). The centre point of both circles is $2.5$cm away from the edge of the diagram. Because there are two circles, you must double the distance and subtract that from $9$ (the key to the second room).

$4 \times 4 = 16$

$16 - 1 = 15$

$15$ is the key to room three.

The Fourth Room:

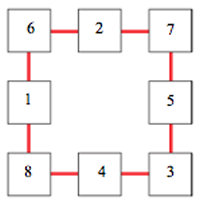
$6 + 7 + 3 + 8 = 24$

$24 - 10 = 14$

The key to the fourth room is $14$.

The Last/Fifth Room:

{There are also two special trays used to cook them in. These hold the key number of tarts each.  There are enough tarts to fill one tray but not enough to fill the other one as well. }

These two sentences suggest that the key number is between $14$ and $28$ (not including $14$ and $28$).

$15$ cannot be the number of tarts as $15$ is divided by $4$ to leave a remainder of $3$. It also is divided by $3$ to leave a remainder of nothing.

We need the remainder to be three when divided by four and a remainder of one when divided by three.

$16$ will leave a remainder of zero when divided by four, so it cannot be the correct number.

$17$ will leave a remainder of one when divided by four, so it cannot be the correct number.

$18$ will leave a remainder of two when divided by four, so it cannot be the correct number.

$19$ will leave a remainder of three when divided by four and a remainder of one when divided by three, so it must by the number of the key.

The key to the last/fifth room is $19$.

The Last Question:

The keys to all the rooms were

1. $13$
2. $9$
3. $15$
4. $14$
5. $19$

1. The 13^th number of the alphabet is m.
2. The 9^th number of the alphabet is i.
3. The 15^th number of the alphabet is o.
4. The 14^th number of the alphabet is n.
5. The 19^th number of the alphabet is s.

Mions

Unscramble the word above to get Simon.

Skippy's real name is Simon.

 

Sam from Shrewsbury House used some slightly different reasoning.  Here is Sam's solution:

Room 1:

The numbers on the top of the dice add up to $8$ below are possible numbers

$1, 2, 5$ -  $1, 3, 4$ -  $1, 1, 6$ -  $2, 2, 4$ - $ 2, 3, 3$

Opposite sides of a die add up to $7$ below are the bottom numbers taking into consideration this fact

$6, 5, 2$ -  $6, 4, 3$ -  $6, 6, 1$ -  $5, 5, 3$ -  $5, 4, 4$

They all equal $13$ so it doesn't matter which set of numbers is on the dice

Therefore the first key is $13$

Room 2:

Cards 1 and 2 = $13$

Cards 2 and 3 = $9$

Cards 3 and 4 = $11$

Cards 4 and 5 = $16$

To work out what the number on the last card is we need to find out what the number on every card is. To do this we need to use trial and improvement

 

The number nine is the key to the second room

Room 3:

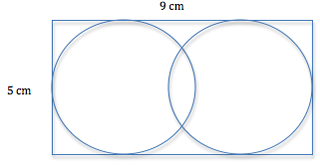
The radius of the circle is half the height of the rectangle

$5 \div2$ is $2.5$

Therefore the radius of the circle is $2.5$cm. The distance between the centres is $9$cm - twice the radius so $9 - 5 = 4$. The distance between the circles therefore is $4$cm

$4 \times 4 = 16$

$16 - 1 = 15$

The third key is $15$

Room 4:

The numbers all have to add up to $15$.  So this means that there either has to be the number $8$ and two numbers that add up to $7$ or vice versa. The $8$ must go with the $6$ and $1$ because the one has to go with the two highest even numbers. There cannot be three even numbers because an even + an even + an even = an even.

Therefore,

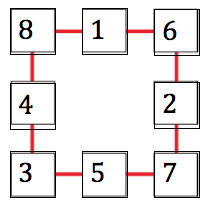
The fourth key number is  $8 + 6 + 7 + 3 - 10=14$

Room 5:

$4 + 4 + 4 + 4 + 3 = 19$

$3 \times 6 +1 = 19$

The key number for room 5 is $19$

 

Skippy's name:

The key numbers are $13, 9, 15, 14, 19$

 

$13$ = M

$9$ = I

$15$ = O

$14$ = N

$19$ = S

M, I, O, N, S

Simon!

 

Hannah from Leicester High School for Girls gave lots of detail about how she tackled each room's challenge.  Here is the Word document which Hannah sent us.  I really like the way Hannah checks her solutions.

Lilith, Bradley, Emily and Jake from Great Torrington Junior clearly communicated their thinking too.  The methods they have used to tackle the problems in the second and fifth rooms are particularly interesting.  Here is Lilith, Bradley and Emily's work:

Key 1: The top and bottom of a die always add up to $7$, so if you had two dice the top and bottom faces would always add up to $14$, three dice would add up to $21$ and so on. All these numbers are multiples of $7$. So for the three dice with the top faces adding up to $8$ then the bottom faces must add up to $13$ as $21 - 8 = 13$.

Key 2: We made lists of the different combinations for each of the totals.

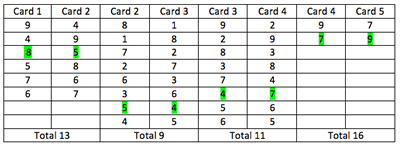
As there are only two possible cards for the last card it is easier to work backwards.  If you have 5^th = $7$, then the 4^th = $9$, 3^rd = $2$, 2^nd = $7$ as you can only use each card once this does not work so it must be a $9$ for the last card. So the order is: $8, 5, 4, 7, 9$, so the answer is $9$.

Key 3: We knew the length of the rectangle was $9$cm and its width was $5$cm. From the bottom of the circles to its centre is half way, which is $2.5$cm, so from the sides to the centre of each circle is $2.5$cm. We took these away from the $9$. So,  $9 - 2.5 - 2.5 = 4$.  $4 \times 4 = 16$. $16 - 1 = 15$.

Key 4: We worked out all the possible combinations of three numbers from $1$  to $8$, which totalled $15$, then we arranged them in the tiles, we soon found out that you could not have the four highest or lowest numbers for the corners, it had to be a combination. $8, 1, 6$; $6, 2, 7$; $7, 3, 5$ and $3, 4, 8$. We found out that the four corners were $8, 6, 3$, and $7$ this totals $24$, we subtracted $10$ and got $14$.

Key 5: We made 2 grids.

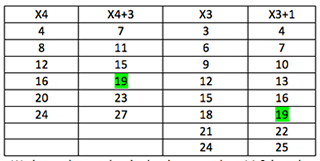
We knew the number had to be more than $14$ and less than $28$ ($2 \times 14$) and must appear in both tables so the answer is $19$

Final question: $13$ = M, $9$ = I, $15$ = o, $14$ = n and $19$ = s when rearranged they spell out SIMON which is Skippy's real name.

A special mention should to the following people who also sent in well-explained solutions:

Aaminah, Sujan, Ahmaan, Bilal, Hasan and Hassan from Arboretum Primary School; Alexi from St Stephen's Junior School; Olga, Amy, Rachel, Bethany, Adam, Abigail, Vicky, and Jade from St Gile's School Killamarsh; Harley and Edward from Great Barford Lower School; Martin from Sutton Grammar School; Year 6 at Highfield School Liphook; Antony from Gaer Junior School; Luke and Alisha at Deneholm Primary, Tom, Thomas, Joshua, Lauren, Cameron, and Jack from Balksbury Junior School; Joe and Kyle at Rudyard Kipling Primary School; Austin and Rushton from Little Heath School; Year 5 at Aboyne Lodge School; Lily, Jess, Andrew and Josiah from Myton; Year 5 at St. Mary's R.C. Primary School, Whickham; Leah at Cavendish Close Junior School; Yasmina, Abidah, Tahmina, Azmina, Samuel, Omar, Miraj and Thanbir from Burnley Brow Community School, Oldham; Makhan and James H from Newtown Maths Group Droxford; Grace, Caitlin, Katie, Brad, Jack and Abbie from Sir Thomas Boughey (Staffordshire); Tom and Ruhan at Dobcroft Junior School, Sheffield; Claire and Simon from Lyneham Primary School.